题目内容
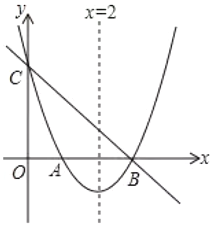
【题目】如图,直线y= -x+3与x轴,y轴分别相交于点B、C,经过B、C两点的抛物线![]() 与x轴的另一交点为A,顶点为P,且对称轴为直线x=2.
与x轴的另一交点为A,顶点为P,且对称轴为直线x=2.
(1)求A点的坐标;
(2)求该抛物线的函数表达式;
(3)连结AC.请问在x轴上是否存在点Q,使得以点P、B、Q为顶点的三角形与△ABC 相似,若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】(1)(1,0)(2)y=x2-4x+3; (3)存在,![]() .
.
【解析】
解:(1)∵直线y=-x+3与x轴相交于点B,
∴当y=0时,x=3,
∴点B的坐标为(3,0).
又∵抛物线过x轴上的A,B两点,且对称轴为x=2,
根据抛物线的对称性,
∴点A的坐标为(1,0).
(2)∵y=-x+3过点C,易知C(0,3),
∴c=3.
又∵抛物线y=ax2+bx+c过点A(1,0),B(3,0),
![]() ,解,得
,解,得![]() ,
,
∴y=x2-4x+3.
(3)连接PB,由y=x2-4x+3=(x-2)2-1,得P(2,-1),
设抛物线的对称轴交x轴于点M,
∵在Rt△PBM中,PM=MB=1,
![]() ,
,
由点B(3,0),C(0,3)易得OB=OC=3,
在等腰直角三角形OBC中,∠ABC=45°,
由勾股定理,得![]() ,
,
假设在x轴上存在点Q,使得以点P,B,Q为顶点的三角形与△ABC相似.
①当![]() 时,△PBQ∽△ABC.
时,△PBQ∽△ABC.
即![]()
∴BQ=3,
又∵BO=3,
∴点Q与点O重合,
∴Q1的坐标是(0,0).
②当![]() ,△QBP∽△ABC.
,△QBP∽△ABC.
即![]() ,
,
![]() ,
,
∵OB=3,
![]() ,
,
∴Q2的坐标是![]() .
.
∵∠PBQ=180°-45°=135°,∠BAC<135°,
∴∠PBQ≠∠BAC.
∴点Q不可能在B点右侧的x轴上
综上所述,在x轴上存在两点![]() ,
,
能使得以点P,B,Q为顶点的三角形与△ABC相似.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目