ЬтФПФкШн
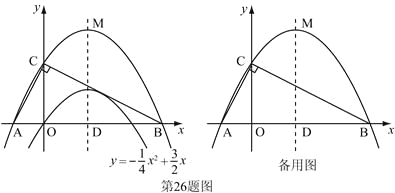
ЁОЬтФПЁПФГЩЬГЁЯњЪлФГжжЦЗХЦЕФЪжЛњ,УПВПНјЛѕМлЮЊ2500дЊ.ЪаГЁЕїбаБэУїЃКЕБЯњЪлМлЮЊ2900дЊЪБ,ЦНОљУПЬьФмЪлГі8ВПЃЛЖјЕБЯњЪлМлУПНЕЕЭ50дЊЪБ,ЦНОљУПЬьОЭФмЖрЪлГі4ВП.
ЃЈ1ЃЉЕБЪлМлЮЊ2800дЊЪБ,етжжЪжЛњЦНОљУПЬьЕФЯњЪлРћШѓДяЕНЖрЩйдЊ?
ЃЈ2ЃЉШєЩшУПВПЪжЛњНЕЕЭxдЊ,УПЬьЕФЯњЪлРћШѓЮЊyдЊ,ЪдаДГіyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ3ЃЉЩЬГЁвЊЯыЛёЕУзюДѓРћШѓ,УПВПЪжЛњЕФЪлМлгІЖЉЮЊЮЊЖрЩйдЊЃПДЫЪБЕФзюДѓРћШѓЪЧЖрЩйдЊЃП
ЁОД№АИЁПЃЈ1ЃЉЕБЪлМлЮЊ2800дЊЪБ,етжжЪжЛњЦНОљУПЬьЕФЯњЪлРћШѓДяЕН4800дЊЃЛ
ЃЈ2ЃЉ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉУПЬЈВЪЕчНЕМл150дЊЪБ,ЩЬГЁУПЬьЯњЪлетжжВЪЕчЕФРћШѓзюДѓ,зюДѓРћШѓЪЧ5000дЊЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉЕБЪлМлЮЊ2800дЊЪБ,ЯњЪлМлНЕЕЭ100дЊ,ЦНОљУПЬьОЭФмЪлГі16ВП.МДПЩЧѓГіУПЬьРћШѓЃЛ
ЃЈ2ЃЉИљОнЃКРћШѓ=ЃЈУПЬЈЪЕМЪЪлМлЉУПЬЈНјМлЃЉЁСЯњЪлСП,УПЬЈЪЕМЪЪлМл=2900Љx,ЯњЪлСП=8+4ЁС![]() ,СаКЏЪ§ЙиЯЕЪНЃЛ
,СаКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉРћгУЖўДЮКЏЪ§ЕФЖЅЕузјБъЙЋЪН,ЧѓКЏЪ§ЕФзюДѓжЕЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЕБЪлМлЮЊ2800дЊЪБ,ЯњЪлМлНЕЕЭ100дЊ,ЦНОљУПЬьОЭФмЪлГі16ВП.
ЫљвдЃКетжжЪжЛњЦНОљУПЬьЕФЯњЪлРћШѓЮЊЃК![]() ЃЈдЊЃЉЃЛ
ЃЈдЊЃЉЃЛ
ЃЈ2ЃЉИљОнЬтвт,ЕУ![]() ,
,
МД![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЖдгк![]() ,
,
ЕБ![]() ЪБ,
ЪБ,
![]()
Ыљвд,УПЬЈВЪЕчНЕМл150дЊЪБ,ЩЬГЁУПЬьЯњЪлетжжВЪЕчЕФРћШѓзюДѓ,зюДѓРћШѓЪЧ5000дЊЃЎ

 ЬьЬьЯђЩЯПкЫуБОЯЕСаД№АИ
ЬьЬьЯђЩЯПкЫуБОЯЕСаД№АИ