题目内容
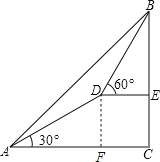
【题目】某测量队在山脚A处测得山上树顶仰角为45°（如图），测量队在山坡上前进600米到D处，再测得树顶的仰角为60°，已知这段山坡的坡角为30°，如果树高为15米，则山高为（ ）（精确到1米， 
=1.732）．
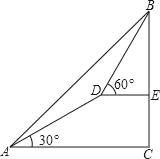
A. 585米 B. 1014米 C. 805米 D. 820米
【答案】C
【解析】过点D作DF⊥AC于F,在直角△ADF中,AF=ADcos30°=300
米,DF=
AD=300米,设FC=x,则AC=300
+x,在直角△BDE中,BE=
DE=
x,则BC=300+
x,在直角△ACB中,∠BAC=45°,∴这个三角形是等腰直角三角形,∴AC=BC,∴300
+x=300+
x,解得:x=300,∴BC=AC=300+300
,∴山高是300+300
-15=285+300
≈805（米）,故选C.
练习册系列答案
相关题目
