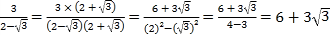题目内容
【题目】某文化用品商店用
元采购一批书包，上市后发现供不应求，很快销售完了.商店又去采购第二批同样款式的书包，进货单价比第一次高
元，商店用了
元，所购数量是第一次的
倍.
（1）求第一批采购的书包的单价是多少元？
（2）若商店按售价为每个书包
元，销售完这两批书包，总共获利多少元？
【答案】（1）第一批采购的书包的单价是80元．（2）销售完这两批书包，总共获利3700元．
【解析】
（1）设第一批采购的书包的单价是x元，则第二批采购的书包的单价是（x+4）元，根据数量=总价÷单价结合第二批购进的数量是第一批的3倍，即可得出关于x的分式方程，解之经检验后即可得出结论；
（2）根据数量=总价÷单价及两次购进数量间的关系，可分别求出第一、二批购进书包的数量，再利用利润=销售单价×数量-进货成本，即可求出结论．
（1）设第一批采购的书包的单价是x元，则第二批采购的书包的单价是（x+4）元，
依题意，得：
，
解得：x=80，
经检验，x=80是所列分式方程的解，且符合题意．
答：第一批采购的书包的单价是80元．
（2）第一批购进书包的数量为2000÷80=25（个），
第二批购进书包的数量为25×3=75（个）．
120×（25+75）-2000-6300=3700（元）．
答：销售完这两批书包，总共获利3700元．
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案【题目】我们约定：如果身高在选定标准的±2%范围之内都称为“普启遍身高”．为了了解某校九年级男生中具有“普遍身高”的人数，我们从该校九年级男生中随机抽出10名男生，分别测量出他们的身高(单位：cm)，收集并整理如下统计表：
男生 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
身高x(cm) | 163 | 171 | 173 | 159 | 161 | 174 | 164 | 166 | 169 | 164 |
根据以上信息，解答如下问题：
(1)计算这组数据的三个统计量：平均数、中位数、众数；
(2)请你选择其中一个统计量作为选定标准，找出这10名男生中具有“普遍身高”是哪几位男生？并说明理由．
【题目】为了倡导“全民阅读”，某校为调查了解学生家庭藏书情况，随机抽取本校部分学生进行调查，并绘制成统计图表如下：
学生家庭藏书情况扇形统计图
类别 | 家庭藏书 | 学生人数 |
|
| 16 |
|
|
|
|
| 50 |
|
| 70 |
根据以上信息，解答下列问题：
（1）共抽样调查了______名学生，
______；
（2）在扇形统计图中，“
”对应扇形的圆心角为_______
；
（3）若该校有2000名学生，请估计全校学生中家庭藏书超过60本的人数.
