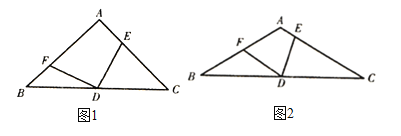
题目内容
【题目】如图,在![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 至点
至点![]() 平分
平分![]() ,且
,且![]() 的延长线交于点
的延长线交于点![]() ,若
,若![]() .
.
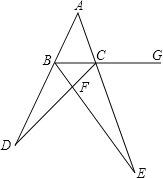
![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 的度数;
的度数;
![]() 若在图中继续作
若在图中继续作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,作
,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,作
,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,以此类推,作
,以此类推,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,请用含有
,请用含有![]() 的式了表示
的式了表示![]() 的度数(直接写答案).
的度数(直接写答案).
【答案】(1)证明见解析;(2)∠E=10°;(3)∠En+l=![]() ∠E.
∠E.
【解析】
(1)根据三角形的一个外角等于和它不相邻的两个内角的和,得出∠DCE=∠A+∠D,∠DFE=∠DCE+∠E,将第一式代入第二式即可得证;
(2)根据角平分线及三角形外角的性质得出∠ECG=![]() ∠DCG=
∠DCG=![]() (∠D+∠DBC),∠ECG=∠E+∠EBC=∠E+
(∠D+∠DBC),∠ECG=∠E+∠EBC=∠E+![]()
∠DBC,则∠D=2∠E,再利用上题结论∠DFE=∠A+∠D+∠E,将已知条件代入,即可求出∠E的度数;
(3)先根据角平分线及三角形外角的性质得出∠E1=![]() ∠E,同理得出∠E2=
∠E,同理得出∠E2=![]() ∠E1,则∠E2=
∠E1,则∠E2=![]() ∠E=
∠E=![]() ∠E,由此得出规律∠En+l=
∠E,由此得出规律∠En+l=![]() ∠E.
∠E.
(1)证明:∵∠DCE=∠A+∠D,∠DFE=∠DCE+∠E,
∴∠DFE=∠A+∠D+∠E;
(2)解:∵∠DCG=∠D+∠DBC,CE平分∠DCG,
∴∠ECG=![]() ∠DCG=
∠DCG=![]() (∠D+∠DBC),
(∠D+∠DBC),
∵BE平分∠DBC,
∴∠EBC=![]() ∠DBC,
∠DBC,
∵∠ECG=∠E+∠EBC=∠E+![]() ∠DBC,
∠DBC,
∴∠E+![]() ∠DBC=
∠DBC=![]() (∠D+∠DBC),
(∠D+∠DBC),
∴∠E=![]() ∠D,
∠D,
∴∠D=2∠E.
∵∠DFE=63°,∠A=33°,∠DFE=∠A+∠D+∠E,
∴∠D+∠E=∠DEF-∠A=63°-33°=30°,
∴
∴∠E=10°;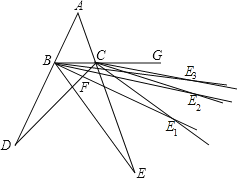
(3)∵∠ECG=∠E+∠EBC,CE1平分∠ECG,
∴∠E1CG=![]() ∠ECG=
∠ECG=![]() (∠E+∠EBC).
(∠E+∠EBC).
∵BE1平分∠EBC,
∴∠E1BC=![]() ∠EBC.
∠EBC.
∵∠E1CG=∠E1+∠E1BC=∠E1+![]() ∠EBC,
∠EBC,
∴∠E1+![]() ∠EBC=
∠EBC=![]() (∠E+∠EBC),
(∠E+∠EBC),
∴∠E1=![]() ∠E.
∠E.
同理:∠E2=![]() ∠E1,
∠E1,
∴∠E2=![]() ∠E=
∠E=![]() ∠E,
∠E,
∴∠En+l=![]() ∠E.
∠E.