题目内容
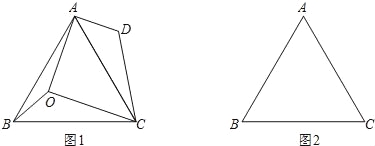
【题目】已知,点O是等边△ABC内的任一点,连接OA,OB,OC.
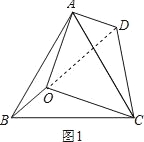
(1)如图1,已知∠AOB=150°,∠BOC=120°,将△BOC绕点C按顺时针方向旋转60°得△ADC.
①∠DAO的度数是 ;
②用等式表示线段OA,OB,OC之间的数量关系,并证明;
(2)设∠AOB=α,∠BOC=β.
①当α,β满足什么关系时,OA+OB+OC有最小值?请在图2中画出符合条件的图形,并说明理由;
②若等边△ABC的边长为1,直接写出OA+OB+OC的最小值.
【答案】(1)90°;②线段OA,OB,OC之间的数量关系是OA2+OB2=OC2,证明见试题解析;
(2)①当α=β=120°时,OA+OB+OC有最小值.证明见试题解析;②线段OA,OB,OC之间的数量关系是OA2+OB2=OC2,证明见试题解析。
【解析】
试题分析:(1)①根据周角的定义得到∠AOC=360°﹣120°﹣150°=90°,由于将△BOC绕点C按顺时针方向旋转60°得△ADC,于是得到∠OCD=60°,∠D=∠BOC=120°,根据四边形的内角和即可得到结论;②如图1,连接OD,由于△BOC绕点C按顺时针方向旋转60°得△ADC,得到△ADC≌△BOC,∠OCD=60°,根据全等三角形的性质得到CD=OC,∠ADC=∠BOC=120°,AD=OB,推出△OCD是等边三角形,根据等边三角形的性质得到OC=OD=CD,∠COD=∠CDO=60°,由于∠AOB=150°,∠BOC=120°,得到∠AOC=90°,求得∠AOD=30°,∠ADO=60°,根据勾股定理即可得到结论;
(2)①如图2,由旋转的性质得到O′C=OC,O′A′=OA,A′C=BC,∠A′O′C=∠AOC..推出△OC O′是等边三角形,根据等边三角形的性质得到OC=O′C=OO′,∠COO′=∠CO′O=60°,由于∠AOB=∠BOC=120°,得到∠AOC=∠A′O′C=120°,推出四点B,O,O′,A′共线,即可得到结论,②根据①的结论即可得到结果.
试题解析:(1)①∠AOB=150°,∠BOC=120°,∴∠AOC=360°﹣120°﹣150°=90°,
∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴∠OCD=60°,∠D=∠BOC=120°,
∴∠DAO=360°﹣∠AOC﹣∠OCD﹣∠D=90°,
故答案为:90°;
②线段OA,OB,OC之间的数量关系是OA2+OB2=OC2,
如图1,连接OD,
∵△BOC绕点C按顺时针方向旋转60°得△ADC,
∴△ADC≌△BOC,∠OCD=60°,∴CD=OC,∠ADC=∠BOC=120°,AD=OB,
∴△OCD是等边三角形,∴OC=OD=CD,∠COD=∠CDO=60°,
∵∠AOB=150°,∠BOC=120°,∴∠AOC=90°,
∴∠AOD=30°,∠ADO=60°,∴∠DAO=90°,
在Rt△ADO中,∠DAO=90°,∴OA2+OB2=OD2,∴OA2+OB2=OC2;
(2)①当α=β=120°时,OA+OB+OC有最小值.
如图2,将△AOC绕点C按顺时针方向旋转60°得△A′O′C,连接OO′,
∴△A′O′C≌△AOC,∠OCO′=∠ACA′=60°,
∴O′C=OC,O′A′=OA,A′C=BC,∠A′O′C=∠AOC.
∴△OC O′是等边三角形,∴OC=O′C=OO′,∠COO′=∠CO′O=60°,
∵∠AOB=∠BOC=120°,∴∠AOC=∠A′O′C=120°,
∴∠BOO′=∠OO′A′=180°,∴四点B,O,O′,A′共线,
∴OA+OB+OC=O′A′+OB+OO′=BA′时值最小;
②∵∠AOB=∠BOC=120°,∴∠AOC=120°,∴O为△ABC的中心,
∵四点B,O,O′,A′共线,∴BD⊥AC,∵将△AOC绕点C按顺时针方向旋转60°得△A′O′C,
∴A′C=AC=BC,∴A′B=2BD,在Rt△BCD中,BD=![]() BC=
BC=![]() ,∴A′B=
,∴A′B=![]() ,
,
∴当等边△ABC的边长为1时,OA+OB+OC的最小值A′B=![]() .
.


 优生乐园系列答案
优生乐园系列答案