题目内容
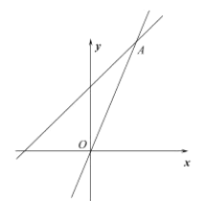
【题目】一次函数![]() 的图像与
的图像与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,以
,以![]() 为边在第二象限内作等边
为边在第二象限内作等边![]() .
.
(1)求![]() 点的坐标;
点的坐标;
(2)在第二象限内有一点![]() ,使
,使![]() ,求
,求![]() 点的坐标;
点的坐标;
(3)将![]() 沿着直线
沿着直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处;再将
处;再将![]() 绕点
绕点![]() 顺时针方向旋转15°,点
顺时针方向旋转15°,点![]() 落在点
落在点![]() 处,过点
处,过点![]() 作
作![]() 轴于
轴于![]() .求
.求![]() 的面积.
的面积.
【答案】(1)C(-2![]() ,4);(2)M(-5
,4);(2)M(-5![]() ,1);(3)2.
,1);(3)2.
【解析】
(1)先求得A、B的坐标,勾股定理求出AB后可得到∠BAO=30°,则∠CAO=90°,从而可得到点C的坐标;
(2)过点C作CM∥AB,则S△ABM=S△ABC.设直线CM的解析式为![]() ,将点C的坐标代入求得b的值,然后将y=1代入MC的解析式可求得点M的横坐标;
,将点C的坐标代入求得b的值,然后将y=1代入MC的解析式可求得点M的横坐标;
(3)先判断出折叠后点C落在y轴上,即E在y轴上.在EG上取一点H,使EH=FH,连接FH.先求出∠FHG=30°,设FG=a,进而表示出EG,用勾股定理建立方程求出a2,最后用面积公式即可得出结论.
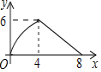
解:(1)当x=0时,y=2,
∴B(0,2).
当y=0时,x=-2 ![]() ,
,
∴A(-2![]() ,0).
,0).
∴OB=2,OA=2![]() ,
,
∴AB=4,
∴∠BAO=30°,
∵△ABC为等边三角形,
∴∠CAB=60°,AC= AB=4.
∴∠CAO=90°.
∴C(-2![]() ,4).
,4).
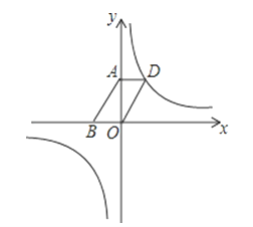
(2)如图1,过点C作CM∥AB.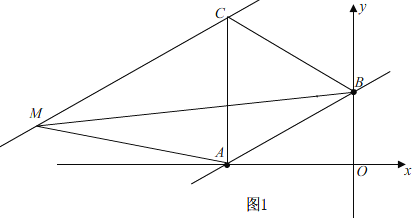
∵CM∥AB,
∴S△ABM=S△ABC.
设直线CM的解析式为![]() ,
,
将点C的坐标代入得![]() ,
,
解得b=6.
∴直线CM的解析式为![]() ,
,
将y=1代入MC的解析式得:![]() ,
,
解得:x=-5![]()
∴M(-5![]() ,1).
,1).
(3)如图2,
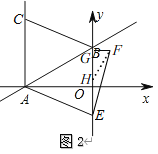
由(1)知A(-2![]() ,0),B(0,2),
,0),B(0,2),
∵△ABC为等边三角形,AB=4,
∴∠CBA=60°,BC=AB=4,
又∠ABO=60°,
∴折叠后点C落在y轴上,即E在y轴上
由折叠知,BE=BC=4,
由旋转知,EF=BE=4,∠BEF=15°,
在EG上取一点H,使EH=FH,连接FH,
∴∠FHG=30°,
设FG=a,
∴HG=![]() a,FH=2a,
a,FH=2a,
∴EH=2a,
∴EG=EH+HG=2a+![]() a=(2+
a=(2+![]() )a,
)a,
在Rt△EFG中,根据勾股定理得,a2+[(2+![]() )a]2=16,
)a]2=16,
∴a2=![]() =
= ![]() ,
,
∴S△EFG![]() EG×FG
EG×FG
=![]() (2+
(2+![]() )a×a
)a×a
![]()
=![]()
=2.