题目内容
【题目】如图,在直角坐标系中,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() ,直线
,直线![]() 过点
过点![]() 且分别交
且分别交![]() 轴负半轴、直线
轴负半轴、直线![]() 于点
于点![]() 、
、![]() ,
,![]() .
.
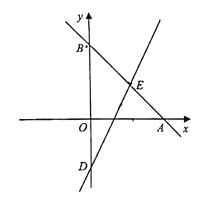
(1)求直线![]() 的解析式及点
的解析式及点![]() 的坐标;
的坐标;
(2)若点![]() 为直线
为直线![]() 上一点,过
上一点,过![]() 作
作![]() 轴,交直线
轴,交直线![]() 于
于![]() ,且点
,且点![]() 的横坐标为
的横坐标为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)直线l2的解析式为:y=2x1,E(1,1);(2)n=![]() 或n=
或n=![]() .
.
【解析】
(1)首先易得A、B的坐标,进而求得D的坐标,然后根据待定系数法求得直线l2的解析式,联立解析式,解方程组即可求得E的坐标;
(2)根据题意列出|n+22n+1|=1,解方程即可求得.
解:(1)由直线l1:y=x+2易得A(2,0),B(0,2),
∴OB=2,
∴OD=![]() OB=1,即D(0,1),
OB=1,即D(0,1),
∵直线l2:y=kx+b过点C(![]() ,2),D(0,1),
,2),D(0,1),
∴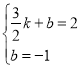 ,解得:
,解得:![]() ,
,
∴直线l2的解析式为:y=2x1,
解方程组![]() 得:
得:![]() ,
,
∴E(1,1);
(2)∵点P为直线l1上一点,点P的横坐标为n,
∴P(n,n+2),
∵过P作PQ∥y轴,交直线l2于Q,
∴Q(n,2n1),
∵BD=3,PQ=![]() BD,
BD,
∴PQ=1,
∴|n+22n+1|=1,
解得:n=![]() 或n=
或n=![]() .
.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目