题目内容
【题目】已知反比例函数y=![]() (m为常数)的图象在一,三象限.
(m为常数)的图象在一,三象限.
(1)求m的取值范围;
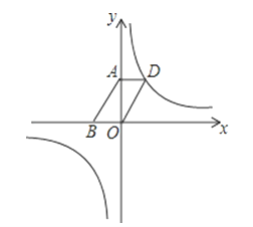
(2)如图,若该反比例函数的图象经过ABOD的顶点D,点A、B的坐标分别为(0,4),(﹣3,0).
①求出函数解析式;
②设点P是该反比例函数图象上的一点,若OD=OP,则P点的坐标为多少?
【答案】(1)m<![]() ;(2)①y=
;(2)①y=![]() ,②(4,3),(﹣3,﹣4),(﹣4,﹣3).
,②(4,3),(﹣3,﹣4),(﹣4,﹣3).
【解析】
(1)根据反比例函数的性质得1-2m>0,然后解不等式即可;
(2)①根据平行四边形的性质得AD∥OB,AD=OB,则可确定D(2,3),然后根据反比例函数图象上点的坐标特征求出k,从而得到解析式;
②利用反比例函数关于原点和直线y=x对称的性质去确定P点坐标.
(1)根据题意得1﹣2m>0,
解得m<![]() ;
;
(2)①∵四边形ABOD为平行四边形,
∴AD∥OB,AD=OB,
而点A,B的坐标分别为(0,4),(﹣3,0),
∴D(3,4);
把D(3,4)代入y=![]() 得k=4×3=12,
得k=4×3=12,
∴反比例函数解析式为y=![]() ,
,
②∵反比例函y=![]() 的图象关于原点对称,
的图象关于原点对称,
而OD=OP时,
∴点D关于原点对称的点为P点,此时P(﹣3,﹣4),
∵反比例函y=![]() 的图象关于直线y=x对称,
的图象关于直线y=x对称,
∴点D关于直线y=x对称的点为P点,此时P(4,3),
同样求出点(4,3)关于原点的对称点(﹣4,﹣3)也满足要求,
∴P点坐标为(4,3),(﹣3,﹣4),(﹣4,﹣3).
故答案为(4,3),(﹣3,﹣4),(﹣4,﹣3).

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目