题目内容
【题目】△ABC中,∠ACB=90°,∠BAC=30°,点C为等边△DEF的边DE的中点.
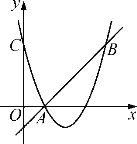
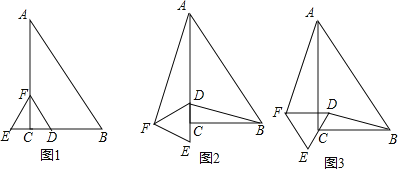
(1)如图1,当DE与BC在同一条直线上时,已知![]() ,求
,求![]() 的值;
的值;
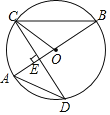
(2)如图2,当DE与AC在同一条直线上时,分别连接AF,BD,试判断BD和AF的位置关系并说明理由;
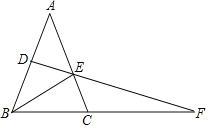
(3)如图3,当DE与△ABC的边均不在一条直线上时,分别连接AF,BD,求证:∠FAC=∠CBD.
【答案】(1)1 (2)BD⊥AF (3)证明见解析
【解析】
(1)根据平行线的判定和平行线线段成比例解答即可;
(2)连接CF,延长BD交AF于G,利用相似三角形的判定和性质解答即可;
(3)连接CF,根据相似三角形的判定和性质解答即可.
(1)∵点C为等边△DEF的边DE的中点,
∴∠EFC=∠CFD=30°,
∵∠BAC=30°,
∴∠CFD=∠BAC,
∴DF∥AB,
∵![]() ,
,
∴![]() ,
,
∵ED=2CD,
∴![]() ;
;
(2)连接CF,延长BD交AF于G,则BD⊥AF于G,如图:
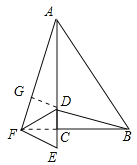
∵![]() ,∠ACF=∠BCD=90°,
,∠ACF=∠BCD=90°,
∴△ACF∽△BCD,
∴∠FAC=∠CBD,
∵∠BDC+∠DBC=90°,
∴∠ADG+∠DAG=90°,
即BD⊥AF于G;
(3)连接CF,如图:
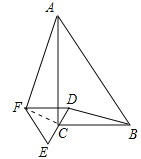
∵点C为等边△DEF的边DE的中点,
∴FC⊥DE,
∴∠FCD=90°,
∵∠FCA+∠ACD=∠BCD+∠ACD=90°,
∴∠FCA=∠BCD,
∵![]() ,
,
∴△ACF∽△BCD,
∴∠FAC=∠CBD.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目