题目内容
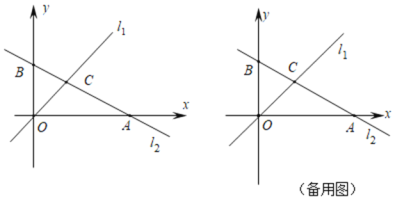
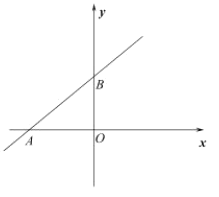
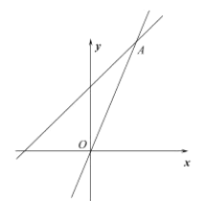
【题目】如图,一次函数![]() 的图像与正比例函数
的图像与正比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像都经过
)的图像都经过![]() .
.
(1)求点![]() 的坐标及正比例函数的表达式;
的坐标及正比例函数的表达式;
(2)利用函数图像比较![]() 和
和![]() 的大小并直接写出对应的
的大小并直接写出对应的![]() 的取值范围.
的取值范围.
【答案】(1)点A坐标为(1,2);y2=2x;(2)当x<1时,y1>y2;当x=1时,y1=y2;当x>1时,y1<y2.
【解析】
(1)将A点代入一次函数解析式求出m的值,然后将A点坐标代入正比例函数解析式,求出k的值即可得出正比例函数的表达式;
(2)结合函数图象即可判断y1和y2的大小及相应的x的取值范围.
解:(1)将A的坐标代入y1=x+1,
得:m+1=2,
解得:m=1,
故点A坐标为(1,2),
将点A的坐标代入:y2=kx,
得:2=k,
解得:k=2,
则反比例函数的表达式y2=2x;
(2)结合函数图象可得:
当x<1时,y1>y2;
当x=1时,y1=y2;
当x>1时,y1<y2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 180 | 260 | 280 | 300 |
y(间) | 100 | 60 | 50 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每间空置的客房,宾馆每日需支出各种费用60元.当房价为多少元时,宾馆当日利润最大?求出最大利润.(宾馆当日利润=当日房费收入-当日支出)