题目内容
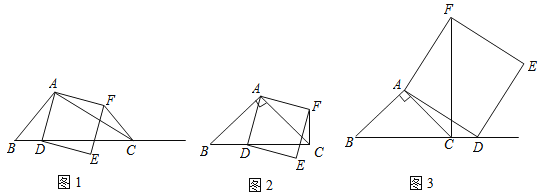
【题目】在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.如果AB=AC,∠BAC=90o,
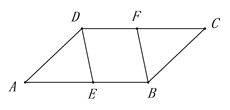
(1)当点D在线段BC上时(与点B不重合),如图2,线段CF 、BD所在直线的位
置关系为 __________,线段CF 、BD的数量关系为 ;
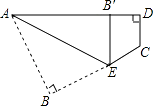
(2)当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由.
【答案】(1)垂直,相等;(2)结论仍成立,理由见解析
【解析】试题分析:(1)由题意可以得出![]() ,∴BD=CF,∠B=∠ACF=45°,∵AB=AC,∠BAC=90o,∴∠BCF=90°,即可得出结论;(2)图3的条件发生变化,但是方法没有发生变化.
,∴BD=CF,∠B=∠ACF=45°,∵AB=AC,∠BAC=90o,∴∠BCF=90°,即可得出结论;(2)图3的条件发生变化,但是方法没有发生变化.
试题解析:
解:(1)垂直,相等;
(2)当点D在BC的延长线上时①的结论仍成立.
由正方形ADEF得 AD=AF ,∠DAF=90.
∵∠BAC=90,∴∠DAF=∠BAC ,∴∠DAB=∠FAC,
又AB=AC ,∴△DAB≌△FAC ,
∴CF=BD , ∠ACF=∠ABD.
∵∠BAC=90, AB=AC ,
∴∠ABC=45,∴∠ACF=45,
∴∠BCF=∠ACB+∠ACF=90.
即 CF⊥BD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目