题目内容
【题目】
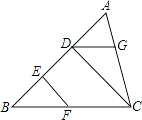
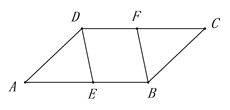
(1)如图，在平行四边形ABCD中，已知点E在AB上，点F在CD上，且AE＝CF．
求证：DE＝BF
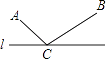
(2)如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠C＝20°，求∠CDA的度数．
【答案】（1）证明见解析；（2）
=125°.
【解析】试题分析：（1）本题利用三角形全等即可求出，或是证明四边形DEBF是平行四边形；（2）本题利用切线的性质得出∠BOD的度数，根据等边对等角，得出∠ADO的度数，即可求出∠CDA的度数．
试题解析：
证明：（方法一）
∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD．
∵AE=CF．
∴BE=FD，BE∥FD，
∴四边形EBFD是平行四边形，
∴DE=BF．
（方法二）
∵四边形ABCD是平行四边形，
∴∠A=∠C，AD=BC,
又∵AE=CF， ∴
，所以DE=BF．
（2）证明：连接
，
∵CD与⊙O相切于点D，
∴OD⊥CD,∴∠ODC=90°
∵
=20°，∴∠COD=70°
∵OA=OD,∴∠ODA=35°
∴
=90°+35°=125°
练习册系列答案
名校课堂系列答案
相关题目
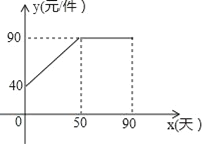
【题目】九年级某班数学兴趣小组经过市场调查整理出某种商品在第x天（1≤x≤90，且x为整数）的售价与销售量的相关信息如下．已知商品的进价为30元/件，设该商品的售价为y（单位：元/件），每天的销售量为p（单位：件），每天的销售利润为w（单位：元）．
时间x（天） | 1 | 30 | 60 | 90 |
每天销售量p（件） | 198 | 140 | 80 | 20 |
（1）求出w与x的函数关系式；
（2）问销售该商品第几天时，当天的销售利润最大？并求出最大利润；
（3）该商品在销售过程中，共有多少天每天的销售利润不低于5600元？请直接写出结果．
