题目内容
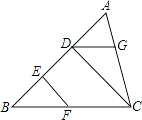
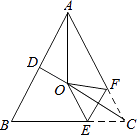
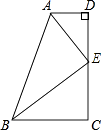
【题目】如图，一个四边形纸片ABCD，∠B=∠D=90°，把纸片按如图所示折叠，使点B落在AD边上的Bˊ点，AE是折痕．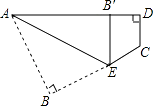 
（1）试判断BˊE与DC的位置关系．
（2）如果∠C=140°，求∠AEB的度数．
【答案】
（1）解：由折叠的性质，得
∠B=∠AB′E=90°，
∴∠AB′E=∠C=90°，
∴B′E∥DC
（2）解：由四边形的一组对角互补，得
∠DAB+∠C=180°．
由∠C=140°得
∠DAB=180°﹣∠C=40°．
由翻折的性质，得
∠BAE= 
∠DAB= ×40°=20°
【解析】（1）根据翻折的性质，可得∠AB′E，根据平行线的判定；（2）根据四边形的性质，可得∠DAB的度数，根据翻折的性质，可得答案．
【考点精析】利用翻折变换（折叠问题）对题目进行判断即可得到答案，需要熟知折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
练习册系列答案
阅读快车系列答案
相关题目
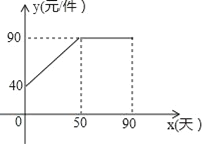
【题目】九年级某班数学兴趣小组经过市场调查整理出某种商品在第x天（1≤x≤90，且x为整数）的售价与销售量的相关信息如下．已知商品的进价为30元/件，设该商品的售价为y（单位：元/件），每天的销售量为p（单位：件），每天的销售利润为w（单位：元）．
时间x（天） | 1 | 30 | 60 | 90 |
每天销售量p（件） | 198 | 140 | 80 | 20 |
（1）求出w与x的函数关系式；
（2）问销售该商品第几天时，当天的销售利润最大？并求出最大利润；
（3）该商品在销售过程中，共有多少天每天的销售利润不低于5600元？请直接写出结果．
