题目内容
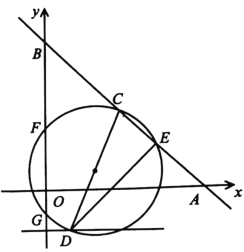
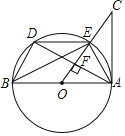
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于E,过点A作AF⊥AC于F交⊙O于D,连接DE,BE,BD
(1)求证:∠C=∠BED;
(2)若AB=12,tan∠BED=![]() ,求CF的长.
,求CF的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据切线性质、垂直的性质、直角三角形的两个锐角互余的性质求得∠C+∠AOC=∠AOC+∠BAD=90°,即∠C=∠BAD;然后由圆周角定理推知∠BED=∠BAD;最后由等量代换得∠C=∠BED;
(2)根据锐角三角函数的定义求出AC,OC的长,求出AF长,则答案可求出.
(1)证明:∵AB是⊙O的直径,CA切⊙O于A,
∴∠C+∠AOC=90°;
又∵OC⊥AD,
∴∠OFA=90°,
∴∠AOC+∠BAD=90°,
∴∠C=∠BAD.
又∵∠BED=∠BAD,
∴∠C=∠BED.
(2)解:由(1)知∠C=∠BAD,tan∠BED=![]() ,
,
∴tan∠C=![]() ,
,
∴tan∠C=![]() ,且OA=
,且OA=![]() AB=6,
AB=6,
∴![]() ,解得AC=8,
,解得AC=8,
∴![]() ,
,
根据∠OFA=∠OAC=90°,
∴OCAF=OAAC,
∴![]() .
.
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目