题目内容
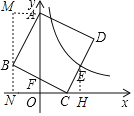
【题目】如图,正方形的顶点A,C分别在y轴和x轴上,边BC的中点F在y轴上,若反比例函数y=![]() 的图象恰好经过CD的中点E,则OA的长为______.
的图象恰好经过CD的中点E,则OA的长为______.

【答案】6
【解析】
证明△CFO≌△CEH,点F是BC的中点,则ON=OC=a,NB=2OF=2b,同理△CNB≌△BMA(AAS),则MA=BN=2b,MB=CN=2a,AM=2b=ON=a,故a=2b,点E(a+b,a),则a(a+b)=6,而a=2b,即可求解.
解:过E作EH⊥x轴于H,连接OE,设:CO=a,CH=b,
过点B作y轴的平行线交x轴于点N,作AM⊥MN于点M,
∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°,
∵∠EHC=∠FCO=90°,
∴∠OFC=∠ECH,
∵点F与点E分别是BC,CD的中点,
∴CF=CE,
∴△CFO≌△CEH(AAS),
点F是BC的中点,则ON=OC=a,NB=2OF=2b,
同理△CNB≌△BMA(AAS),
则MA=BN=2b,MB=CN=2a,
AM=2b=ON=a,故a=2b,
点E(a+b,a),则a(a+b)=6,而a=2b,
解得:b=1,a=2,
OA=MN=BM+BN=2a+2b=6,
故答案为:6.

【题目】根据扬州市某风景区的旅游信息,![]() 公司组织一批员工到该风景区旅游,支付给旅行社
公司组织一批员工到该风景区旅游,支付给旅行社![]() 元.
元. ![]() 公司参加这次旅游的员工有多少人?
公司参加这次旅游的员工有多少人?
扬州市某风景区旅游信息表
旅游人数 | 收费标准 |
不超过 | 人均收费 |
超过 | 每增加 |
【题目】从甲地到乙地有![]() 三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时的频数 公交车用时线路 |
|
|
|
| 合计 |
| 59 | 151 | 166 | 124 | 500 |
| 50 | 50 | 122 | 278 | 500 |
| 45 | 265 | 160 | 30 | 500 |
早高峰期间,乘坐_________(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
【题目】某生物课外活动小组的同学进行植物标本制作比赛,结果统计如下表:
每人所制 作标本数 | 2 | 4 | 6 | 8 | 10 |
人数 | 1 | 2 | 4 | 3 | 2 |
请根据表中信息,回答下列问题:
(1)该活动小组共有学生多少人?
(2)制作标本数在6个及以上的人数占小组总人数的百分比是多少?
(3)根据统计表制作一个合适的统计图来描述这次比赛的结果.