Question

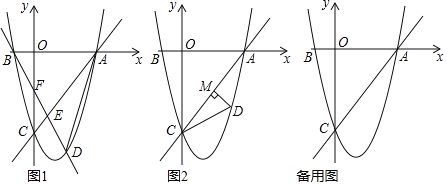
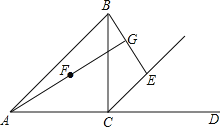
【题目】如图直线与x轴、y轴分别交于点A，B，C是的中点，点D在直线上，以为直径的圆与直线的另一交点为E，交y轴于点F，G，已知，，则的长是______．

Answer 1

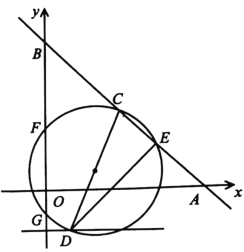
【答案】

【解析】

如图，设CD的中点为O′，设直线BA交直线y＝﹣2于M，直线y＝﹣2交y轴于P，作CH⊥OB于H，连接O′F，作AJ⊥DM于J，O′N⊥FG于N．首先利用等腰直角三角形的性质和条件可确定A，B，C的坐标，再设D（m，﹣2），进而可得O′N与O′F的长，而FN＝，然后在Rt△O′FN中利用勾股定理构建方程即可求出m，问题即得解决．

解：如图，设CD的中点为O′，设直线BA交直线y＝﹣2于M，直线y＝﹣2交y轴于P，作CH⊥OB于H，连接O′F，作AJ⊥DM于J，O′N⊥FG于N．

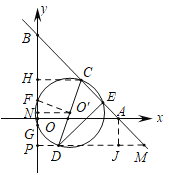
∵CD是⊙O′的直径，∴∠CED＝90°，

∵直线y＝﹣x+m（m＞0）与x轴、y轴分别交于点A，B，

∴A（m，0），B（0，m），

∴OA＝OB，∴∠OAB＝45°，

∵OA∥DM，∴∠EMD＝∠OAB＝45°，

∵∠DEM＝90°，∴ED＝EM，

∴EC+ED＝EC+EM＝CM＝，

∵JA⊥DM，∴∠AJM＝90°，

∴AJ＝JM＝2，AM＝2，

∴BC＝CA＝4，∴AB＝8，∴BO＝AO＝8，

∴A（8，0），B（0，8），C（4，4），

设D（m，﹣2），则O′（（m+4），1），

∴O′N＝（m+4），O′F＝CD＝，

∵O′N⊥FG，∴FN＝，

在Rt△O′FN中，由勾股定理，得：，解得m＝1，

∴CD＝．

故答案为：．