题目内容
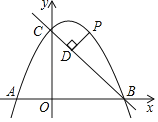
【题目】如图,抛物线 y=﹣x2+bx+c 与 x 轴交于 A、B 两点,与 y 轴交于点 C ,点 A 的坐标为(-1,0),点 C 的坐标为(0,3),点D和点 C 关于抛物线的对称轴对称,直线 AD 与 y 轴交于点 E .
(1)求抛物线的解析式;
(2)如图,直线 AD 上方的抛物线上有一点 F,过点 F 作 FG⊥AD 于点 G,作 FH 平行于 x 轴交直线 AD 于点 H,求△FGH 周长的最大值.
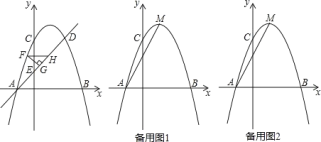
【答案】(1)y=﹣x2+2x+3;(2)△FGH周长最大值为:![]() .
.
【解析】
(1)利用待定系数法求解即可;
(2)根据抛物线的解析式可得对称轴的方程,即可求出点D的坐标,利用待定系数法可得直线AD的解析式,即可求出点E的坐标,得△OAE是等腰直角三角形,由FH 平行于 x 轴可得△FGH为等腰直角三角形过点 F 作 FM⊥x 轴交 AD 于 M,可得△FMH是等腰直角三角形,即可得出△FGH的周长等于△FGM的周长,配方可求出FM的最大值,即可得出△FGM周长的最大值,进而可得答案.
(1)将 (-1,0), (0,3)代入y=﹣x2+bx+c ,得:
-1-b+c=0,c=3,解得:b=2,c=3,
即抛物线的解析式为:y=﹣x2+2x+3.
(2)∵y=﹣x2+2x+3
=﹣(x﹣1)2+4,
∴抛物线对称轴为直线 x=1,点 D 和点 C 关于直线x=1对称,
∴D(2,3),
设直线 AD 的解析式为 y=kx+b,
把 A(﹣1,0),D(2,3)代入得:
![]() ,解得
,解得![]() ,
,
∴直线AD的解析式为:y=x+1;
∴E(0,1),
∵OA=OE,
∴△OAE 为等腰直角三角形,
∴∠EAO=45°,
∵FH∥OA,△FGH 为等腰直角三角形,
过点 F 作 FM⊥x 轴交 AD 于 M,如图,
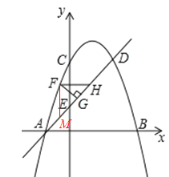
可得FM=FH,
∵FG=GH=![]() FH=
FH=![]() FM,
FM,
∴C△FGH=(1+![]() )FM,
)FM,
设F(m,﹣m2+2m+3),则M(m,m+1),FM=﹣m2+m+2
∴C△FGH=(1+![]() )FM,
)FM,
=(1+![]() )(﹣m2+m+2)
)(﹣m2+m+2)
=﹣(1+![]() )
)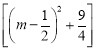
∴当 x=![]() 时,△FGH周长由最大值,最大值为:
时,△FGH周长由最大值,最大值为:![]() .
.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案