Question

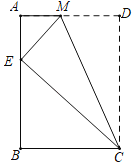
【题目】如图将矩形ABCD沿CM折叠，使点D落在AB边上的点E处，

（1）求证：△AME∽△BEC．

（2）若△EMC∽△AME，求AB与BC的数量关系．

Answer 1

【答案】（1）详见解析；（2）．

【解析】

（1）根据两角对应相等的两个三角形相似即可证明．

（2）利用相似三角形的性质证明∠BCE＝∠ECM＝∠DCM＝30°即可解决问题．

（1）∵矩形ABCD，

∴∠A＝∠B＝∠D＝90°，

∵将矩形ABCD沿CM折叠，使点D落在AB边上的点E处，

∴∠MEC＝∠D＝90°，

∴∠AEM+∠BEC＝90°，

∵∠AEM+∠AME＝90°，

∴∠AME＝∠EBC，

又∵∠A＝∠B，

∴△AME∽△BEC．

（2）∵△EMC∽△AME，

∴∠AEM＝∠ECM，

∵△AME∽△BEC，

∴∠AEM＝∠BCE，

∴∠BCE＝∠ECM

由折叠可知：△ECM≌△DCM，

∴∠DCM＝∠ECM，DC＝EC，

即∠BCE＝∠ECM＝∠DCM＝30°，

在Rt△BCE中，，

∴，

∵DC＝EC＝AB，

∴.