题目内容
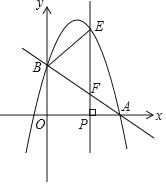
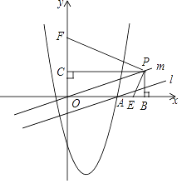
【题目】如图:在平面直角坐标系中,直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,经过点
,经过点![]() 的抛物线
的抛物线![]() 的对称轴是
的对称轴是![]() .
.
(1)求抛物线的解析式.
(2)平移直线![]() 经过原点
经过原点![]() ,得到直线
,得到直线![]() ,点
,点![]() 是直线
是直线![]() 上任意一点,
上任意一点,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,若点
,若点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() ,
,![]() ,且
,且![]() .求证:
.求证:![]() .
.
(3)若(2)中的点![]() 坐标为
坐标为![]() ,点
,点![]() 是
是![]() 轴上的点,点
轴上的点,点![]() 是
是![]() 轴上的点,当
轴上的点,当![]() 时,抛物线上是否存在点
时,抛物线上是否存在点![]() ,使四边形
,使四边形![]() 是矩形?若存在,请求出点
是矩形?若存在,请求出点![]() 的坐标,如果不存在,请说明理由.
的坐标,如果不存在,请说明理由.
【答案】(1)![]() ;(2)证明见解析;(3)存在,点
;(2)证明见解析;(3)存在,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)先求得点A的坐标,然后依据抛物线过点A,对称轴是![]() ,列出关于a、c的方程组求解即可;
,列出关于a、c的方程组求解即可;
(2)设P(3n,n),则PC=3n,PB=n,然后再证明∠FPC=∠EPB,最后通过等量代换进行证明即可;
(3)设![]() ,然后用含t的式子表示BE的长,从而可得到CF的长,于是可得到点F的坐标,然后依据中点坐标公式可得到
,然后用含t的式子表示BE的长,从而可得到CF的长,于是可得到点F的坐标,然后依据中点坐标公式可得到![]() ,
,![]() ,从而可求得点Q的坐标(用含t的式子表示),最后,将点Q的坐标代入抛物线的解析式求得t的值即可.
,从而可求得点Q的坐标(用含t的式子表示),最后,将点Q的坐标代入抛物线的解析式求得t的值即可.
解:(1)当![]() 时,
时,![]() ,
,
解得![]() ,即
,即![]() ,
,
抛物线过点![]() ,对称轴是
,对称轴是![]() ,
,
得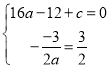 ,
,
解得![]() ,抛物线的解析式为
,抛物线的解析式为![]() ;
;
(2)∵平移直线![]() 经过原点
经过原点![]() ,得到直线
,得到直线![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
∵点![]() 是直线
是直线![]() 上任意一点,
上任意一点,
∴![]() ,则
,则![]() ,
,![]() .
.
又∵![]() ,
,
∴![]() .
.
∵![]() 轴,
轴,![]() 轴
轴
∴![]()
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
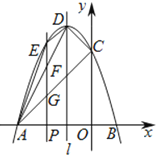
(3)设![]() ,点
,点![]() 在点
在点![]() 的左侧时,如图所示,则
的左侧时,如图所示,则![]() .
.
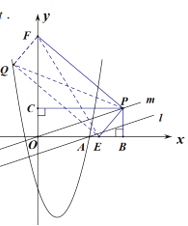
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵四边形![]() 为矩形,
为矩形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
将点![]() 的坐标代入抛物线的解析式得:
的坐标代入抛物线的解析式得:![]() ,
,
解得:![]() 或
或![]() (舍去).
(舍去).
∴![]() .
.
当点![]() 在点
在点![]() 的右侧时,如下图所示,则
的右侧时,如下图所示,则![]() .
.
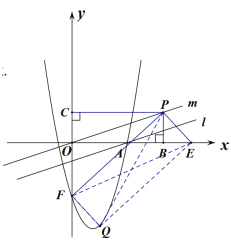
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵四边形![]() 为矩形,
为矩形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
将点![]() 的坐标代入抛物线的解析式得:
的坐标代入抛物线的解析式得:![]() ,
,
解得:![]() 或
或![]() (舍去).
(舍去).
∴![]() .
.
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目