题目内容
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,若将直线
两点,若将直线![]() 向右平移
向右平移![]() 个单位得到直线
个单位得到直线![]() ,
,![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
(1)求点![]() 的坐标;
的坐标;
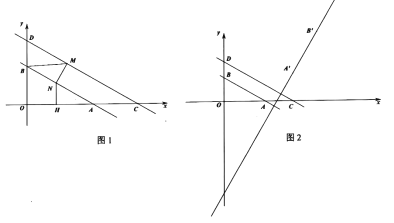
(2)如图1,若点![]() 是直线
是直线![]() 上一动点,且
上一动点,且![]() ,
,![]() 轴,连接
轴,连接![]() ,求
,求![]() 的最小值及此时点
的最小值及此时点![]() 的坐标;
的坐标;
(3)如图2,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() ,延长线段
,延长线段![]() 得到直线
得到直线![]() ,线段
,线段![]() 在直线
在直线![]() 上移动,当以点
上移动,当以点![]() 、
、![]() 、
、![]() 构成的三角形是等腰三角形时,直接写出点
构成的三角形是等腰三角形时,直接写出点![]() 的坐标.
的坐标.
【答案】(1)D(0,5);(2)![]() +
+![]() ;N(
;N(![]() ,
,![]() );(3)A'(
);(3)A'(![]() ,
,![]() ),A'(
),A'(![]() ,
,![]() );A'(
);A'(![]() ,
,![]() ),A'(
),A'(![]() ,
,![]() );A'(5
);A'(5![]() -
-![]() ,-
,-![]() );
);
【解析】
(1)求出直线L2:y=-![]() x+5即可求出D;
x+5即可求出D;
(2)求出两直线间距离MN=![]() ,作B点关于L2的对称点B',与L2的交点为F,过点F作FH⊥x轴,交于L1于N,过点N作MN⊥L2,则BM+MN+NH的最小值即为
,作B点关于L2的对称点B',与L2的交点为F,过点F作FH⊥x轴,交于L1于N,过点N作MN⊥L2,则BM+MN+NH的最小值即为![]() +FH;过点B作BG⊥FH,在Rt△BGF中,∠FBG=60°,BF=
+FH;过点B作BG⊥FH,在Rt△BGF中,∠FBG=60°,BF=![]() ,求出F(
,求出F(![]() );在Rt△BNG中,∠GBN=30°,BG=
);在Rt△BNG中,∠GBN=30°,BG=![]() ,求出N(
,求出N(![]() ,
,![]() ),则可求FH=
),则可求FH=![]() ,即可德奥BM+MN+NH的最小值
,即可德奥BM+MN+NH的最小值![]() +
+![]() ;
;
(3)由已知可知,AC⊥A'C,AC=A'C,求得A'(5![]() ,2
,2![]() ),再由直线L1与直线L3垂直,可求直线L3:y=
),再由直线L1与直线L3垂直,可求直线L3:y=![]() x+2
x+2![]() -15,设A'(m,
-15,设A'(m,![]() m+2
m+2![]() -15),则B'(m+3,
-15),则B'(m+3,![]() m+5
m+5![]() -15),
-15),
①当A'B'=A'C时,A'C=6,所以36=(m5![]() )2+(
)2+(![]() m+2
m+2![]() 15)2;②当A'B'=B'C时,B'C=6,所以36=(m+35
15)2;②当A'B'=B'C时,B'C=6,所以36=(m+35![]() )2+(
)2+(![]() m+5
m+5![]() 15)2,③当A'C=B'C时,(m5
15)2,③当A'C=B'C时,(m5![]() )2+(
)2+(![]() m+2
m+2![]() 15)2=(m+35
15)2=(m+35![]() )2+(
)2+(![]() m+5
m+5![]() 15)2span>,分别求出m即可.
15)2span>,分别求出m即可.
(1)由已知可得A(3![]() ,0),B(0,3),
,0),B(0,3),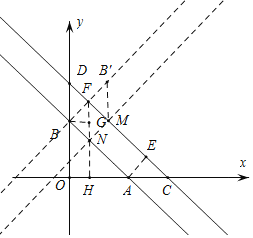
∵将直线l1向右平移2![]() 个单位得到直线L2,
个单位得到直线L2,
∴C(5![]() ,0),
,0),
∴直线L2:y=![]() x+5,
x+5,
∴D(0,5);
(2)过点A作AE⊥L2,
∵AC=2![]() ,∠DCA=30°,
,∠DCA=30°,
∴AE=![]() ,
,
∴MN=![]() ,
,
∴BM+MN+NH的最小值即为BM+![]() +NH的最小值,
+NH的最小值,
作B点关于L2的对称点B',与L2的交点为F,过点F作FH⊥x轴,交于L1于N,过点N作MN⊥L2,
则BM+MN+NH的最小值即为![]() +FH;
+FH;
由作图可得,四边形FNMB'是平行四边形,
∴B'M=FN,
∵B与B'关于L2对称,
∴BM=B'M,
∴BM=FN,
在Rt△BDF中,BF=![]() ,BD=2,
,BD=2,
∴∠DBF=30°,
过点B作BG⊥FH,
在Rt△BGF中,∠FBG=60°,BF=![]() ,
,
∴GB=![]() ,FG=
,FG=![]() ,
,
∴F(![]() ,
,![]() ),
),
在Rt△BNG中,∠GBN=30°,BG=![]() ,
,
∴GN=![]() ,
,
∴N(![]() ,
,![]() ),
),
∴FH=![]() ,
,
∴BM+MN+NH的最小值![]() +
+![]() ;
;
(3)由已知可知,AC⊥A'C,AC=A'C,
∴A'(5![]() ,2
,2![]() ),
),
∵直线L1与直线L3垂直,
∴直线L3:y=![]() x+2
x+2![]() -15,
-15,
∵A(3![]() ,0),B(0,3),
,0),B(0,3),
∴AB=6,
设A'(m,![]() m+2
m+2![]() -15),则B'(m+3,
-15),则B'(m+3,![]() m+5
m+5![]() -15),
-15),
①当A'B'=A'C时,A'C=6,
∴36=(m5![]() )2+(
)2+(![]() m+2
m+2![]() 15)2
15)2
∴m=![]() 或m=
或m=![]() ,
,
∴A'(![]() ,
,![]() ),A'(
),A'(![]() ,
,![]() );
);
②当A'B'=B'C时,B'C=6,
∴36=(m+35![]() )2+(
)2+(![]() m+5
m+5![]() 15)2,
15)2,
∴m=![]() 或m=
或m=![]() ;
;
∴A'(![]() ,
,![]() ),A'(
),A'(![]() ,
,![]() );
);
③当A'C=B'C时,
(m5![]() )2+(
)2+(![]() m+2
m+2![]() 15)2=(m+35
15)2=(m+35![]() )2+(
)2+(![]() m+5
m+5![]() 15)2,
15)2,
∴m=5![]() -
-![]() ;
;
∴A'(5![]() -
-![]() ,-
,-![]() );
);
综上所述A'(![]() ,
,![]() ),A'(
),A'(![]() ,
,![]() );
);
,A'(![]() ,
,![]() ),A'(
),A'(![]() ,
,![]() );
);
;A'(5![]() -
-![]() ,-
,-![]() );
);