题目内容
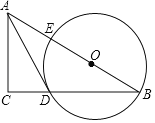
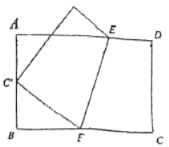
【题目】如图,将矩形![]() 沿
沿![]() 折叠,使顶点
折叠,使顶点![]() 恰好落在
恰好落在![]() 边的中点
边的中点![]() 处,若
处,若![]() ,
,![]() ,则
,则![]() 的长为___________.
的长为___________.
【答案】6
【解析】
先根据勾股定理求出BF,再根据△AMC′∽△BC′F求出AM、MC′、MD′,再证明△MAC′≌△MD′E,可得EM=MC′即可解决问题.
解:根据折叠的性质可知,FC=FC′,∠C=∠FC′M=90°,

设BF=x,则FC=FC′=9-x,
∵BF2+BC′2=FC′2,
∴x2+32=(9-x)2,
解得:x=4,
∵∠FC′M=90°,
∴∠AC′M+∠BC′F=90°,
又∵∠BFC′+BC′F=90°,
∴∠AC′M=∠BFC′
∵∠A=∠B=90°
∴△AMC′∽△BC′F
∴![]() ,
,
∵BC′=AC′=3,
∴AM=![]() ,
,
∴MC′=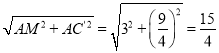 ,
,
∴D′M=6-![]() =
=![]() ,
,
∴AM=MD′,
∵∠A=∠D′=90°,∠AMC′=∠EMD′,
∴△MAC′≌△MD′E,
∴EM=MC′=![]() ,
,
∴AE=AM+EM=![]() ,
,
故答案为6.

练习册系列答案
相关题目