Question

【题目】由甲、乙两个工程队承包某校园绿化工程，已知甲、乙两队单独完成这项工程所需时间比是2：3，且两队合作6天可以完成．

（1）求甲、乙两队单独完成此工程分别需要多少天？

（2）甲队工作一天需付报酬3500元，乙队工作一天需付报酬2000元，学校需要在9天内完成绿化工作，学校该如何安排甲、乙两队工作时间，才能使得所付报酬最少？最少报酬是多少？

Answer 1

【答案】（1）甲、乙两队单独完成此工程分别需要10天、15天；（2）甲乙两队合作4天，乙队单独干5天，学校付报酬最低，最低32000元．

【解析】

（1）设甲队单独完成此工程需x天，则可表示出乙队单独完成此工程需天，利用工作量为1列方程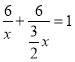，再解方程、检验，然后计算即可；

（2）设甲队干了m天，乙队干了n天，则，通过代换得到报酬的一次函数关系式，利用不等式的关系求解即可．

设甲队单独完成此工程需x天，则乙队单独完成此工程需天，

根据题意得，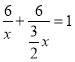

解得x=10，

经检验x=10是原方程的解，

当x=10时，=15，

答：甲、乙两队单独完成此工程分别需要10天、15天，

故答案为：10；15；

（2）设甲、乙两队合作干了m天，然后乙队又单独干了n天，则

，，

解得m=6-，

代入不等式得，6-+n9，

解得：n5，

学校需要付的报酬为：

（3500+2000）m+2000n=5500m+2000n=33000-2200n+2000n=33000-200n，

∵-200<0，n值越大，学校付的报酬越少，

∴n=5时，原式=33000-1000=32000（元），

此时m=4，

答：甲乙合作4天，然后乙队单独干5天，学校付的报酬最低，最低32000元，

故答案为：甲乙两队合作4天，乙队单独干5天，学校付报酬最低，最低32000元．