题目内容
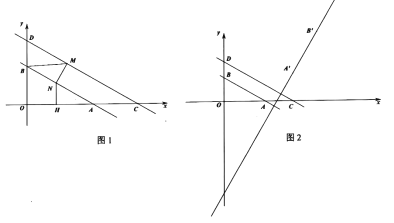
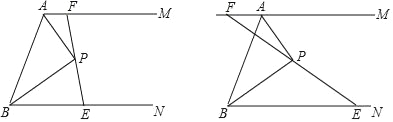
【题目】如图,AM∥BN,∠MAB和∠NBA的角平分线相交于点P,过点P作直线EF分别交AM、BN于F、E.
(1)求证:AB=AF+BE;
(2)若EF绕点P旋转,F在MA的延长线上滑动,如图,请你测量,猜想AB、AF、BE之间的关系,写出这个关系式,并加以证明.
【答案】(1)证明见解析;(2)见解析.
【解析】
(1)延长AP交BE于Q,求出AB=BQ,根据BP平分∠ABE求出AP=PQ,推出AF=EQ,即可得出答案;
(2)①求出AB=BQ,根据BP平分∠ABE求出AP=PQ,推出AF=EQ,即可得出答案;
②延长AP交BE于Q,同①可得AB=BQ,再求出AF=EQ,即可得出答案.
(1)延长AP交BE于Q,
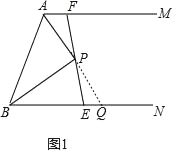
∵AP平分∠MAB,
∴∠MAP=∠BAP,
∵AM∥BN,
∴∠MAP=∠AQB,
∴∠BAP=∠AQB,
∴AB=BQ,
∵BP平分∠ABE,
∴AP=PQ,
∵AM∥BN,
∴![]() =
=![]() =1,
=1,
∴AF=EQ,
∴AB=AF+BE;
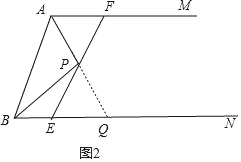
(2)①成立,
如图2,

延长AP交BE于Q,
∵AP平分∠MAB,
∴∠MAP=∠BAP,
∵AM∥BN,
∴∠MAP=∠AQB,
∴∠BAP=∠AQB,
∴AB=BQ,
∵BP平分∠ABE,
∴AP=PQ,
∵AM∥BN,
∴![]() =
=![]() =1,
=1,
∴AF=EQ,
∴AB=AF+BE;
②不同,猜想:AF+AB=BE,
证明:延长AP交BE于Q,
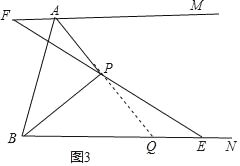
∵AP平分∠MAB,
∴∠MAP=∠BAP,
∵AM∥BN,
∴∠MAP=∠AQB,
∴∠BAP=∠AQB,
∴AB=BQ,
∵BP平分∠ABE,
∴AP=PQ,
∵AM∥BN,
∴![]() =
=![]() =1,
=1,
∴AF=EQ,
∴AF+AB=BE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目