题目内容
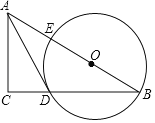
【题目】如图,正方形![]() 的边长为10,
的边长为10,![]() ,
,![]() ,连接
,连接![]() ,则线段
,则线段![]() 的长为( )
的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
延长DH交AG于点E,利用SSS证出△AGB≌△CHD,然后利用ASA证出△ADE≌△DCH,根据全等三角形的性质求出EG、HE和∠HEG,最后利用勾股定理即可求出HG.
解:延长DH交AG于点E

∵四边形ABCD为正方形
∴AD=DC=BA=10,∠ADC=∠BAD=90°
在△AGB和△CHD中
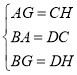
∴△AGB≌△CHD
∴∠BAG=∠DCH
∵∠BAG+∠DAE=90°
∴∠DCH+∠DAE=90°
∴CH2+DH2=82+62=100= DC2
∴△CHD为直角三角形,∠CHD=90°
∴∠DCH+∠CDH=90°
∴∠DAE=∠CDH,
∵∠CDH+∠ADE=90°
∴∠ADE=∠DCH
在△ADE和△DCH中

∴△ADE≌△DCH
∴AE=DH=6,DE=CH=8,∠AED=∠DHC=90°
∴EG=AG-AE=2,HE= DE-DH=2,∠GEH=180°-∠AED=90°
在Rt△GEH中,GH=![]()
故选B.

练习册系列答案
相关题目