题目内容
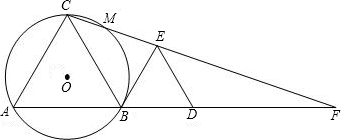
如图,B为线段AD上一点,△ABC和△BDE都是等边三角形,连接CE并延长交AD的延长线于点F,△ABC的外接圆⊙O交CF于点M.
(1)求证:BE是⊙O的切线;
(2)求证:AC2=CM•CF;
(3)若CM=
,MF=
,求BD;
(4)若过点D作DG∥BE交EF于点G,过G作GH∥DE交DF于点H,则易知△DGH是等边三角形.设等边△ABC、△BDE、△DGH的面积分别为S1、S2、S3,试探究S1、S2、S3之间的等量关系,请直接写出其结论.
(1)求证:BE是⊙O的切线;
(2)求证:AC2=CM•CF;
(3)若CM=
2
| ||
| 7 |
12
| ||
| 7 |
(4)若过点D作DG∥BE交EF于点G,过G作GH∥DE交DF于点H,则易知△DGH是等边三角形.设等边△ABC、△BDE、△DGH的面积分别为S1、S2、S3,试探究S1、S2、S3之间的等量关系,请直接写出其结论.

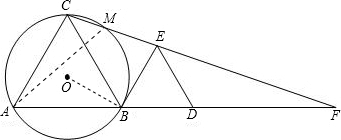
(1)证明:连接OB
∵△ABC和△BDE都是等边三角形
∴AB=BC=AC,∠CAB=∠ABC=∠EBD=60°
∴∠OBC=30°(1分)
∵∠CBE=180°-60°-60°=60°
∴∠OBE=30°+60°=90°即OB⊥BE(2分)
∴BE是⊙O的切线;(3分)
(2)证明:连接AM,则∠AMC=∠ABC=∠CAF=60°(4分)
∵∠ACM=∠FCA
∴△ACM∽△FCA(5分)
∴
=
∴AC2=CM•CF;(6分)
(3)∵AC2=CM•CF
∴AC=2(7分)
设FB=x
∵FB•FA=FM•FC
∴x(x+2)=
•2
∴x=4,x=-6(舍去)
∴FB=4(8分)
∵EB∥AC
∴
=
∴
=
(9分)
∴BE=
∴BD=
;(10分)
(4)S22=S1•S3或
=
(12分).
∵△ABC和△BDE都是等边三角形
∴AB=BC=AC,∠CAB=∠ABC=∠EBD=60°
∴∠OBC=30°(1分)
∵∠CBE=180°-60°-60°=60°
∴∠OBE=30°+60°=90°即OB⊥BE(2分)
∴BE是⊙O的切线;(3分)
(2)证明:连接AM,则∠AMC=∠ABC=∠CAF=60°(4分)
∵∠ACM=∠FCA
∴△ACM∽△FCA(5分)
∴
| AC |
| CF |
| CM |
| AC |
∴AC2=CM•CF;(6分)
(3)∵AC2=CM•CF
∴AC=2(7分)
设FB=x
∵FB•FA=FM•FC
∴x(x+2)=
12
| ||
| 7 |
| 7 |
∴x=4,x=-6(舍去)
∴FB=4(8分)
∵EB∥AC
∴
| BE |
| AC |
| FB |
| FA |
∴
| BE |
| 2 |
| 4 |
| 6 |
∴BE=
| 4 |
| 3 |
∴BD=
| 4 |
| 3 |
(4)S22=S1•S3或
| S1 |
| S2 |
| S2 |
| S3 |


练习册系列答案
相关题目





 限,点C的坐标为(0,-2),过B点作BE⊥CD于点E.
限,点C的坐标为(0,-2),过B点作BE⊥CD于点E.