题目内容
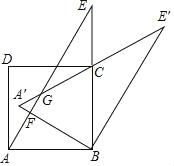
【题目】在平面内,给定∠AOB=60°,及OB边上一点C,如图所示.到射线OA,OB距离相等的所有点组成图形G,线段OC的垂直平分线交图形G于点D,连接CD.
(1)依题意补全图形;直接写出∠DCO的度数;
(2)过点D作OD的垂线,交OA于点E,OB于点F.求证:CF=DE.

【答案】(1)见解析,30°;(2)见解析
【解析】
(1)根据角平分的判定定理可知图形G为∠AOC的平分线,是一条射线,据此补全图形;再根据垂直平分线和角平分线的性质转化角即可求出∠DCO的度数.
(2)通过中间线段DF进行转化可证得结论,即可先证明CF=DF,再证明DE=DF即可.
解:(1)根据角平分的判定定理可知图形G为∠AOC的平分线,是一条射线.补全图形如图1所示:

∠1,∠2,∠3,∠4,如图2所示,
∵OD是∠AOB的平分线,∠AOB =60°,
∴∠1 =∠2=30°,
又∵点D在OC的垂直平分线上,
∴CD=OD,
∴∠3 =∠2=30°.
即∠DCO=30°.
(2) 证明:∵EF⊥OD,
∴∠EDO =∠FDO =90°,
∴∠DFO =60°,又∠3=30°,
∴∠4 =30°,∴∠4 =∠3,
∴CF=DF,
又易得△OED≌△OFD,
∴DE=DF,
∴CF=DE.

练习册系列答案
相关题目