题目内容

【题目】如图1，把圆形井盖卡在角尺〔角的两边互相垂直，一边有刻度）之间，即圆与两条直角边相切，现将角尺向右平移10cm，如图2，OA边与圆的两个交点对应CD的长为40cm则可知井盖的直径是（ ）

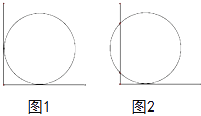
A. 25cm B. 30cm C. 50cm D. 60cm

【答案】C

【解析】

设井盖的直径为2xcm，则BE=10cm，BO=（x﹣10）cm，BC=20cm，CO=xcm．在Rt△BCO中，根据勾股定理得：CO2=BC2+BO2，然后代入即可解出x的值，求出井盖的直径．

过O作OB⊥OA于B，交⊙O于点E，连接OC．如下所示：

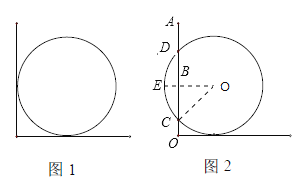
设井盖的直径为2xcm，则BE=10cm，BO=（x﹣10）cm，BC=20cm，CO=xcm．在Rt△BCO中，根据勾股定理得：CO2=BC2+BO2，代入得：x2=202+（x﹣10）2，解得：x=25，则井盖的直径是50cm．

故选C．

练习册系列答案
相关题目

【题目】如图，已知△ABC中，∠ABC=45°，点D是BC边上一动点（与点B，C不重合），点E与点D关于直线AC对称，连结AE，过点B作BF⊥ED的延长线于点F．

（1）依题意补全图形；

（2）当AE=BD时，用等式表示线段DE与BF之间的数量关系，并证明．

【题目】在中，，翻折，使点落在斜边上某一点处，折痕为（点、分别在边、上）

当时，若与相似（如图），求的长；

当点是的中点时（如图），与相似吗？请说明理由．

【题目】如图1，点C在线段AB上，（点C不与A、B重合），分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE，连接AE、BD交于点P．

（观察猜想）

①AE与BD的数量关系是　 　；

②∠APD的度数为　 　．

（数学思考）

如图2，当点C在线段AB外时，（1）中的结论①、②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明；

（拓展应用）

如图3，点E为四边形ABCD内一点，且满足∠AED＝∠BEC＝90°，AE＝DE，BE＝CE，对角线AC、BD交于点P，AC＝10，则四边形ABCD的面积为　 　．

【题目】随机掷两枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，则这两枚骰子向上的一面点数都是奇数的概率是 ．

【题目】某校九年级有600名学生，在体育中考前进行了一次模拟体测.从中随机抽取部分学生，根据其测试成绩制作了下面两个统计图.请根据相关信息，解答下列问题：

（Ⅰ）本次抽取到的学生人数为 ，图2中的值为 ；

（Ⅱ）求本次调查获取的样本数据的平均数、众数和中位数；

（Ⅲ）根据样本数据，估计该校九年级模拟体测中得12分的学生约有多少人？

【题目】如图，点P在长方形OABC的边OA上，连接BP，过点P作BP的垂线，交射线OC于点Q，在点P从点A出发沿AO方向运动到点O的过程中，设AP=x，OQ=y，则下列说法正确的是（ ）

A.y随x的增大而增大B.y随x的增大而减小

C.随x的增大，y先增大后减小D.随x的增大，y先减小后增大

【题目】在Rt△ABC中，∠ACB=90°，AC=15，AB=25，点D为斜边AB上动点．

（1）如图1，当CD⊥AB时，求CD的长度；

（2）如图2，当AD=AC时，过点D作DE⊥AB交BC于点E，求CE的长度；

（3）如图3，在点D的运动过程中，连接CD，当△ACD为等腰三角形时，直接写出AD的长度．

【题目】学校为了调查学生对教学的满意度，随机抽取了部分学生作问卷调查：用“A”表示“很满意“，“B”表示“满意”，“C”表示“比较满意”，“D”表示“不满意”，如图甲、乙是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图，请你根据统计图提供的信息解答以下问题：

（1）本次问卷调查，共调查了多少名学生？

（2）将图甲中“B”部分的图形补充完整；

（3）如果该校有学生1000人，请你估计该校学生对教学感到“不满意”的约有多少人？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网