题目内容
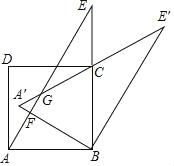
【题目】如图,把正方形ABCD和Rt△ABE重叠在一起,其中AB=2,∠BAE=60°,若把Rt△ABE绕直角顶点B按顺时针方向旋转,使斜边AE恰好经过正方形的顶点C,得到Rt△A′BE′,AE与A′B、A′E分别相交于点F,G,那么△ABE与△A′BE′的重叠部分(即四边形BCGF部分)的面积为_____.
【答案】6﹣![]()
【解析】
可证明△A’BC是等边三角形,并且可证明∠A’FG=90°,故可求出△A’BC和△A’FG的面积,从而求出四边形BCGF的面积.
∵∠BAE=∠BA’E’,AB=A’B=BC,∴△A’BC是等边三角形,∴∠A’BC=60°,∴∠ABA’=30°,∵∠BAE=∠BA’E’=60°,∴∠A’FG=∠AFB=90°,∠A’GF=∠EGC=30°,而∠E=30°=∠EGC,∴CG=EC,在Rt△ABE中,∵AB=BC=2,∠BAE=60°,∴BE=2![]() ,∴CG=EC=BE-BC=2
,∴CG=EC=BE-BC=2![]() -2,∴A’G=A’C-CG=2-(2
-2,∴A’G=A’C-CG=2-(2![]() -2)=4-2
-2)=4-2![]() ,在Rt△A’GF中,∠A’GF=30°,∴A’F=2-
,在Rt△A’GF中,∠A’GF=30°,∴A’F=2-![]() ,FG=2
,FG=2![]() -3,故△A’FG的面积=
-3,故△A’FG的面积=![]() ×A’F×FG=
×A’F×FG=![]() ,而根据等边三角形面积公式可求出△A’BC的面积=
,而根据等边三角形面积公式可求出△A’BC的面积=![]() ,∴S四边形BCGF=S△A’BC-S△A’FG=
,∴S四边形BCGF=S△A’BC-S△A’FG=![]() -(
-(![]() )=6-
)=6-![]() ,故答案为=6-
,故答案为=6-![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某学校计划在总费用2300元的限额内,租用客车送234名学生和6名教师集体外出活动,每辆客车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 45 | 30 |
租金/(元/辆) | 400 | 280 |
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.
【题目】对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,他们将全部测试成绩分成A、B、C、D四组,绘制了如下统计图表:
“垃圾分类知识及投放情况”问卷测试成绩统计图表
组别 | 分数/分 | 频数 | 各组总分/分 |
A | 60<x≤70 | 38 | 2 581 |
B | 70<x≤80 | 72 | 5 543 |
C | 80<x≤90 | 60 | 5 100 |
D | 90<x≤100 | m | 2 796 |

依据以上统计信息,解答下列问题:
(1)求得m=________,n=__________;
(2)这次测试成绩的中位数落在______组;
(3)求本次全部测试成绩的平均数.