Question

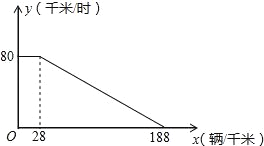
【题目】经研究表明，某市跨河大桥上的车流速度V（单位：千米/时）是车流密度x（单位：辆/千米）的函数，函数图象如图所示．

（1）求当28≤x≤188时，关于x的函数表达式；

（2）求车流量P（单位：辆/时）与车流密度x之间的函数关系式；（注：车流量是单位时间内通过观测点的车辆数，计算公式为：车流量=车流速度×车流密度）

（3）若车流速度V不低于50千米时，求当车流密度x为多少时，车流量P达到最大，并求出这一最大值．

Answer 1

【答案】（1）V=﹣x+94；（2）P=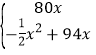；（3）当x=88时，P取得最大为4400．

【解析】

（1）根据题意列方程组即可得到结论；

（2）根据题意即可求得函数的解析式；

（3）根据二次函数的性质即可得到结论．

（1）由图象可知，当28≤x≤188时，

V是x的一次函数，设函数解析式为V=kx+b，

则，

解得，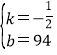

所以V=-x+94；

（2）当0≤x≤28时，P=Vx=80x；

当28≤x≤188时，P=Vx=（-x+94）x=-x2+94x，

所以P=；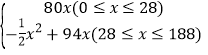

（3）当V≥50时，包含V=80，由函数图象可知，

当V=80时，0＜x≤28，此时P=80x，P随x的增大而增大，

当x=28时，P最大=2240；

由题意得，V=-x+94≥50，解得：x≤88，

又P=-x2+94x，

当28≤x≤88时，P随x的增大而增大，

即当x=88时，P取得最大值，

故P最大=-×882+94×88=4400，

∵2240＜4400，

所以当x=88时，P取得最大为4400．