题目内容
【题目】在△ABC中,AB=AC,点D为射线CB上一个动点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作EF∥BC,交直线AC于点F,连接CE.
⑴如图1,若∠BAC=60°,求证:△CEF是等边三角形.
⑵若∠BAC<60°.
①如图2,当点D在线段CB上移动时,判断△CEF为等腰三角形并证明;
②当点D在线段CB的延长线上移动时,△CEF是什么三角形?请你在图3中画出相应的图形并直接写出结论(不必证明).

【答案】(1)见解析;(2)①证明见解析;②△CEF为等腰三角形,证明见解析
【解析】
(1)根据题意推出△ABC为等边三角形,然后通过求证△ABD≌△ACE,结合平行线的性质,即可证得结论;
(2)①根据(1)的推理依据,求证△ABD≌△ACE,结合平行线的性质,即可证得结论;
②根据题意画出图形,利用(1)的推理依据,求证△ABD≌△ACE,再利用等角的补角相等,,结合平行线的性质,即可证得结论.
证明:⑴ ∵AB=AC,∠BAC=60![]()
∴△ABC为等边三角形,
在△ABD和△ACE中:
∠BAD=60![]() -∠DAC
-∠DAC
∠CAE=60O-∠DAC
∴ ∠BAD=∠CAE
又∵AB=AC,AD=AE
∴△ABD≌△ACE
∴∠ACE= ∠ABD=60![]()
又∵ EF∥BC
∴∠EFC= ∠ACB=60![]()
∴∠FEC=60![]()
∴△CEF是等边三角形
⑵ ①△CEF为等腰三角形,理由如下:
∵AB=AC
∴∠ABC=∠ACB
在△ABD和△ACE中:
∠BAD=∠BAC-∠DAC
∠CAE=∠DAE-∠DAC
而∠DAE=∠BAC
∴ ∠BAD=∠CAE
又∵AB=AC,AD=AE
∴△ABD≌△ACE
∴∠ABC=∠ACE
又∵EF∥BC
∴ ∠EFC= ∠ACB
而∠ABC=∠ACB
∴∠EFC= ∠ECF
所以,△CEF为等腰三角形.
②当点D在线段CB的延长线上时 ,
△CEF为等腰三角形,如图3
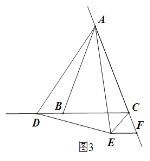
理由如下:
∵AB=AC
∴ ∠ABC=∠ACB
在△ABD和△ACE中:
∠BAD=∠DAE -∠BAE
∠CAE=∠BAC -∠BAE
而∠DAE=∠BAC
∴ ∠BAD=∠CAE
又∵AB=AC,AD=AE
∴△ABD≌△ACE
∴∠ABD=∠ACE
∴∠ABC=∠ECF (等角的补角相等)
又∵EF∥BC
∴∠EFC= ∠ACB
而∠ABC=∠ACB
∴∠EFC= ∠ECF
所以,△CEF为等腰三角形.

【题目】某学校计划在总费用2300元的限额内,租用客车送234名学生和6名教师集体外出活动,每辆客车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 45 | 30 |
租金/(元/辆) | 400 | 280 |
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.





