题目内容
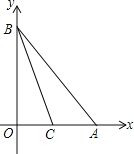
【题目】如图,点A和点B分别在x轴和y轴上,且OA=OB=4,直线BC交x轴于点C,S△BOC=S△ABC.
(1)求直线BC的解析式;
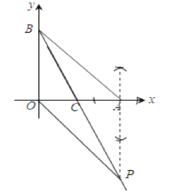
(2)在直线BC上求作一点P,使四边形OBAP为平行四边形(尺规作图,保留痕迹,不写作法).
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)根据三角形面积公式得到OC=AC=![]() OA=2,则C(2,0),然后利用待定系数法求直线BC的解析式;
OA=2,则C(2,0),然后利用待定系数法求直线BC的解析式;
(2)当AP⊥x轴时,AP∥OB,利用OC=AC可得到AP=OB,根据平行四边形的判定方法可得到四边形OBAP为平行四边形,于是过点A作x轴的垂线交直线BC于P即可.
(1)依题意,A(4,0),B(0,4),
因为S△BOC=S△ABC,所以,C为OA中点,所以,C(2,0),
设直线BC的解析式为:![]() ,则有
,则有
![]() ,所以,k=-2,b=4,
,所以,k=-2,b=4,
直线BC的解析式为:![]()
(2)过点A作AP垂直x轴,交BC的延长线于P,连结OP,点P为所求.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目