题目内容
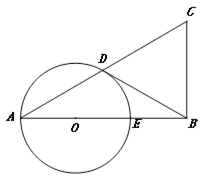
【题目】在平面内,给定不在同一直线上的点A,B,C,如图所示.点O到点A,B,C的距离均等于a(a为常数),到点O的距离等于a的所有点组成图形G,![]() 的平分线交图形G于点D,连接AD,CD.
的平分线交图形G于点D,连接AD,CD.
(1)求证:AD=CD;
(2)过点D作DE![]() BA,垂足为E,作DF
BA,垂足为E,作DF![]() BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.
BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.
【答案】依题意画出图形G为⊙O,如图所示,见解析;(1)证明见解析;(2)直线DE与图形G的公共点个数为1个.
【解析】
(1)根据线段垂直平分线的性质得出图形G为⊙O,再根据在同圆或等圆中相等的圆周角所对的弧相等得出![]() ;从而得出弦相等即可.
;从而得出弦相等即可.
(2)先根据HL得出△CDF≌△CMF,得出DF=MF,从而得出BC为弦DM的垂直平分线,根据圆心角和圆周角之间的关系定理得出∠ABC=∠COD,再证得
DE为⊙O的切线即可
如图所示,依题意画出图形G为⊙O,如图所示
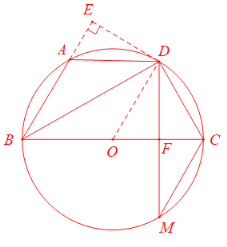
(1)证明:∵BD平分∠ABC,∴∠ABD=∠CBD,
∴![]() ,∴AD=CD
,∴AD=CD
(2)解:∵AD=CD,AD=CM,∴CD=CM.∵DF⊥BC,∴∠DFC=∠CFM=90°
在Rt△CDF和Rt△CMF中
![]() ,∴△CDF≌△CMF(HL),∴DF=MF,∴BC为弦DM的垂直平分线
,∴△CDF≌△CMF(HL),∴DF=MF,∴BC为弦DM的垂直平分线
∴BC为⊙O的直径,连接OD
∵∠COD=2∠CBD,∠ABC=2∠CBD,∴∠ABC=∠COD,∴OD∥BE.
又∵DE⊥BA,∴∠DEB=90°,∴∠ODE=90°,即OD⊥DE,∴DE为⊙O的切线.
∴直线DE与图形G的公共点个数为1个.

 阅读快车系列答案
阅读快车系列答案【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.