题目内容
【题目】如图,一次函数![]() 的图像经过点A(-1,0),并与反比例函数
的图像经过点A(-1,0),并与反比例函数![]() (
(![]() )的图像交于B(m,4)
)的图像交于B(m,4)

(1)求![]() 的值;
的值;
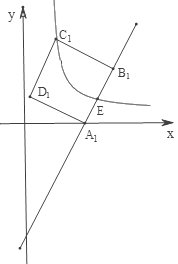
(2)以AB为一边,在AB的左侧作正方形![]() ,求C点坐标;
,求C点坐标;
(3)将正方形![]() 沿着
沿着![]() 轴的正方向,向右平移n个单位长度,得到正方形
轴的正方向,向右平移n个单位长度,得到正方形![]() ,线段
,线段![]() 的中点为点
的中点为点![]() ,若点
,若点![]() 和点
和点![]() 同时落在反比例函数
同时落在反比例函数![]() 的图像上,求n的值.
的图像上,求n的值.
【答案】(1)k1=4;(2)C点坐标为(-3,6);(3)n=![]() .
.
【解析】
(1)把A点坐标代入y=2x+b,可求出b值,把B(m,4)代入可求出m值,代入![]() 即可求出k1的值;(2)过B作BF⊥x轴于F,过C作CG⊥FB,交FB的延长线于G,利用AAS可证明△CBG≌△BAF,可得AF=BG,CG=BF,根据A、B两点坐标即可得C点坐标;(3)由A、B、C三点坐标可得向右平移n个单位后A1、B1、C1的坐标,即可得E点坐标,根据k2=xy列方程即可求出n值.
即可求出k1的值;(2)过B作BF⊥x轴于F,过C作CG⊥FB,交FB的延长线于G,利用AAS可证明△CBG≌△BAF,可得AF=BG,CG=BF,根据A、B两点坐标即可得C点坐标;(3)由A、B、C三点坐标可得向右平移n个单位后A1、B1、C1的坐标,即可得E点坐标,根据k2=xy列方程即可求出n值.
(1)∵一次函数![]() 的图像经过点A(-1,0),
的图像经过点A(-1,0),
∴-2+b=0,
解得:b=2,
∵点B(m,4)在一次函数y=2x+2上,
∴4=2m+2,
解得:m=1,
∵B(1,4)在反比例函数![]() 图象上,
图象上,
∴k1=4.
(2)如图,过B作BF⊥x轴于F,过C作CG⊥FB,交FB的延长线于G,
∵A(-1,0),B(1,4),
∴AF=2,BF=4,
∴∠GCB+∠CBG=90°,
∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠ABF+∠CBG=90°,
∴∠GCB=∠ABF,
又∵BC=AB,∠AFB=∠CGB=90°,
∴△CBG≌△BAF,
∴BG=AF=2,CG=BF=4,
∴GF=6,
∵在AB的左侧作正方形ABCD,
∴C点坐标为(-3,6).
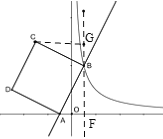
(3)∵正方形ABCD沿x轴的正方向,向右平移n个单位长度,
∴A1(-1+n,0),B1(1+n,4),C1(-3+n,6),
∵线段A1B1的中点为点E,
∴E(n,2),
∵点![]() 和点E同时落在反比例函数
和点E同时落在反比例函数![]() 的图像上,
的图像上,
∴k2=2n=6(-3+n)
解得:n=![]() .
.