Question

【题目】如图，△ABC中，∠ACB=90°，AC=BC，点E是AC上一点，连接BE．

（1）如图1，若AB=，BE=5，求AE的长；

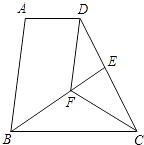
（2）如图2，点D是线段BE延长线上一点，过点A作AF⊥BD于点F，连接CD、CF，当AF=DF时，求证：DC=BC．

Answer 1

【答案】（1）1；（2）证明见解析．

【解析】

试题分析：（1）根据等腰直角三角形的性质得到AC=BC=AB=4，根据勾股定理得到CE==3，于是得到结论；

（2）根据等腰直角三角形的性质得到∠CAB=45°，由于∠AFB=∠ACB=90°，推出A，F，C，B四点共圆，根据圆周角定理得到∠CFB=∠CAB=45°，求得∠DFC=∠AFC=135°，根据全等三角形的性质即可得到结论．

试题解析：（1）∵∠ACB=90°，AC=BC，∴AC=BC=AB=4，∵BE=5，∴CE==3，∴AE=4﹣3=1；

（2）∵∠ACB=90°，AC=BC，∴∠CAB=45°，∵AF⊥BD，∴∠AFB=∠ACB=90°，∴A，F，C，B四点共圆，∴∠CFB=∠CAB=45°，∴∠DFC=∠AFC=135°，在△ACF与△DCF中，∵AF=DF，∠AFC=∠DFC，CF=CF，∴△ACF≌△DCF，∴CD=AC，∵AC=BC，∴AC=BC．