题目内容
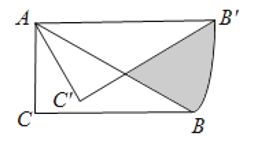
【题目】已知在△ABC中,∠B=90o,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
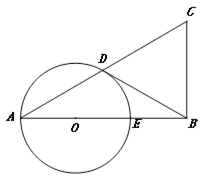
(1)求证:AC·AD=AB·AE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
【答案】(1)证明见解析;(2)AC=4.
【解析】
(1)连接DE,由题意可得∠ADE=90°,∠ABC=90°,又∠A是公共角,从而可得△ADE∽△ABC,由相似比即可得;
(2)连接OB,由BD是切线,得OD⊥BD,有E为OB中点,则可得OE=BE=OD,从而可得∠OBD=∠BAC=30°,所以AC=2BC=4;
(1)连接DE,∵AE是直径,∴∠ADE=90o,∴∠ADE=∠ABC,在Rt△ADE和Rt△ABC中,∠A是公共角,∴△ADE∽△ABC,∴![]() ,即AC·AD=AB·AE
,即AC·AD=AB·AE
(2)连接OD,∵BD是圆O的切线,则OD⊥BD,在Rt△OBD中,OE=BE=OD
∴OB=2OD,∴∠OBD=30°,同理∠BAC=30°,在Rt△ABC中,AC=2BC=2×2=4.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
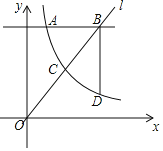
小学生10分钟应用题系列答案【题目】在二次函数的学习中,教材有如下内容:
例1 函数图象求一元二次方程![]() 的近似解(精确到0.1).
的近似解(精确到0.1).
解:设有二次函数![]() ,列表并作出它的图象(图1).
,列表并作出它的图象(图1).
| … |
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| … |
|
|
|
|
|
|
| … |
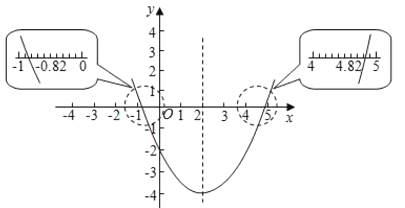
观察抛物线和![]() 轴交点的位置,估计出交点的横坐标分别约为
轴交点的位置,估计出交点的横坐标分别约为![]() 和4.8,所以得出方程精确到0.1的近似解为
和4.8,所以得出方程精确到0.1的近似解为![]() ,
,![]() ,利用二次函数
,利用二次函数![]() 的图象求出一元二次方程
的图象求出一元二次方程![]() 的解的方法称为图象法,这种方法常用来求方程的近似解.
的解的方法称为图象法,这种方法常用来求方程的近似解.
小聪和小明通过例题的学习,体会到利用函数图象可以求出方程的近似解.于是他们尝试利用图象法探宄方程![]() 的近似解,做法如下:
的近似解,做法如下:
小聪的做法:令函数![]() ,列表并画出函数的图象,借助图象得到方程
,列表并画出函数的图象,借助图象得到方程![]() 的近似解.
的近似解.
小明的做法:因为![]() ,所以先将方程
,所以先将方程![]() 的两边同时除以
的两边同时除以![]() ,变形得到方程
,变形得到方程![]() ,再令函数
,再令函数![]() 和
和![]() ,列表并画出这两个函数的图象,借助图象得到方程
,列表并画出这两个函数的图象,借助图象得到方程![]() 的近似解.
的近似解.
请你选择小聪或小明的做法,求出方程![]() 的近似解(精确到0.1).
的近似解(精确到0.1).