Question

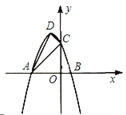
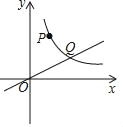
【题目】如图所示，直线y＝x与反比例函数y＝（k≠0，x＞0）的图象交于点Q（4，a），点P（m，n）是反比例函数图象上一点，且n＝2m．

（1）求点 P坐标；

（2）若点M在x轴上，使得△PMQ的面积为3，求M坐标．

Answer 1

【答案】（1）P（2，4）；（2）M坐标（3，0）或（9，0）.

【解析】

（1）先将点Q坐标代入y＝x，求出a的值，再代入y＝求出k的值，再将点P坐标代入反比例函数解析式即可．
（2）延长PQ交x轴于A，连接QM，根据待定系数法求出直线PQ解析式，从而求得点A的坐标，设M（n，0）根据S△PQM=S△PAM-S△QAM 列出方程即可得M坐标．

解：（1）∵直线y＝x与反比例函数y＝（k≠0，x＞0）的图象交于点Q（4，a），

∴a＝×4＝2，

a＝

∴k＝8

∴反比例函数y＝（x＞0）

∵点P（m，n）是反比例函数图象上一点，

∴mn＝8，且n＝2m，m＞0

∴m＝2，n＝4

∴P（2，4）

（2）延长PQ交x轴于A，连接OM，

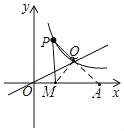
设直线PQ解析式y＝kx+b，

∴

解得：

∴解析式y＝﹣x+6，

∵直线PQ交x轴于A，

∴A（6，0），

设M（n，0）且△PMQ的面积为3

∵S△PQM＝S△PAM﹣S△QAM

∴3＝|6﹣n|×4﹣|6﹣n|×2，

∴n＝3或n＝9，

∴M坐标（3，0）或（9，0）