��Ŀ����
����Ŀ����ͼ����֪������y����x2+bx+c��һֱ���ཻ��A��1��0����C����2��3�����㣬��y�ύ�ڵ�N���䶥��ΪD��
��1����������ֱ��AC�ĺ�����ϵʽ��
��2����P����������λ��ֱ��AC�Ϸ���һ�����㣬����APC����������ֵ����ʱ��P�����ꣻ
��3���ڶԳ������Ƿ����һ��M��ʹ��ANM���ܳ���С�������ڣ������M����������ANM�ܳ�����Сֵ���������ڣ���˵�����ɣ�

���𰸡���1��y����x2��2x+3��y����x+1����2����x����![]() ʱ����APC�����ȡ���ֵ�����ֵΪ
ʱ����APC�����ȡ���ֵ�����ֵΪ![]() ����ʱ��P������Ϊ����
����ʱ��P������Ϊ����![]() ��
��![]() ������3���ڶԳ����ϴ���һ��M����1��2����ʹ��ANM���ܳ���С����ANM�ܳ�����СֵΪ3
������3���ڶԳ����ϴ���һ��M����1��2����ʹ��ANM���ܳ���С����ANM�ܳ�����СֵΪ3![]() ��
��
��������
��1�����ݵ�A��C�����꣬���ô���ϵ�����������������ֱ��AC�ĺ�����ϵʽ����2������P��PE��y�ύx���ڵ�E����ֱ��AC�ڵ�F������C��CQ��y�ύx���ڵ�Q�����P������Ϊ��x����x2��2x+3������2��x��1�������E������Ϊ��x��0������F������Ϊ��x����x+1���������ɵó�PF��ֵ���ɵ�C������ɵó���Q�����꣬�����ɵó�AQ��ֵ�����������ε������ʽ�ɵó�S��APC����![]() x2��
x2��![]() x+3�������ö��κ��������ʣ����ɽ����ֵ���⣻��3�����ö��κ���ͼ���ϵ�����������ɵó���N�����꣬�����䷽�����ҳ������ߵĶԳ��ᣬ�ɵ�C��N������ɵó���C��N���������ߵĶԳ���Գƣ���ֱ��AC�������ߵĶԳ���Ľ���Ϊ��M�����ʱ��ANM�ܳ�ȡ��Сֵ��������һ�κ���ͼ���ϵ���������������M�����꣬�Լ����������ľ��빫ʽ��������ε��ܳ���ʽ�����ANM�ܳ�����Сֵ���ɵó����ۣ�
x+3�������ö��κ��������ʣ����ɽ����ֵ���⣻��3�����ö��κ���ͼ���ϵ�����������ɵó���N�����꣬�����䷽�����ҳ������ߵĶԳ��ᣬ�ɵ�C��N������ɵó���C��N���������ߵĶԳ���Գƣ���ֱ��AC�������ߵĶԳ���Ľ���Ϊ��M�����ʱ��ANM�ܳ�ȡ��Сֵ��������һ�κ���ͼ���ϵ���������������M�����꣬�Լ����������ľ��빫ʽ��������ε��ܳ���ʽ�����ANM�ܳ�����Сֵ���ɵó����ۣ�
��1����A��1��0����C����2��3������y����x2+bx+c���ã�
![]() ����ã�
����ã�![]() ��
��
�������ߵĺ�����ϵʽΪy����x2��2x+3��
��ֱ��AC�ĺ�����ϵʽΪy��mx+n��m��0����
��A��1��0����C����2��3������y��mx+n���ã�
![]() ����ã�
����ã�![]() ��
��
��ֱ��AC�ĺ�����ϵʽΪy����x+1��
��2������P��PE��y�ύx���ڵ�E����ֱ��AC�ڵ�F������C��CQ��y�ύx���ڵ�Q����ͼ1��ʾ��
���P��������x����x2��2x+3������2��x��1�������E��������x��0������F��������x����x+1����
��PE����x2��2x+3��EF����x+1��EF��PE��EF����x2��2x+3������x+1������x2��x+2��
����C����������2��3����
����Q����������2��0����
��AQ��1������2����3��
��S��APC��![]() AQPF����
AQPF����![]() x2��
x2��![]() x+3����
x+3����![]() ��x+
��x+![]() ��2+
��2+![]() ��
��
����![]() ��0��
��0��
����x����![]() ʱ����APC�����ȡ���ֵ�����ֵΪ
ʱ����APC�����ȡ���ֵ�����ֵΪ![]() ����ʱ��P������Ϊ����
����ʱ��P������Ϊ����![]() ��
��![]() ����
����
��3����x��0ʱ��y����x2��2x+3��3��
����N��������0��3����
��y����x2��2x+3������x+1��2+4��
�������ߵĶԳ���Ϊֱ��x����1��
����C����������2��3����
����C��N���������ߵĶԳ���Գƣ�
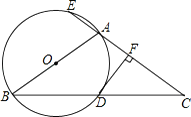
��ֱ��AC�������ߵĶԳ���Ľ���Ϊ��M����ͼ2��ʾ��
����C��N���������ߵĶԳ���Գƣ�
��MN��CM��
��AM+MN��AM+MC��AC��
����ʱ��ANM�ܳ�ȡ��Сֵ��
��x����1ʱ��y����x+1��2��
����ʱ��M������Ϊ����1��2����
����A��������1��0������C����������2��3������N��������0��3����
��AC��![]() ��3
��3![]() ��AN��
��AN��![]() ��
��![]() ��
��
��C��ANM��AM+MN+AN��AC+AN��3![]() +
+![]() ��
��
���ڶԳ����ϴ���һ��M����1��2����ʹ��ANM������С����ANM�ܳ�����СֵΪ3![]() +
+![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�