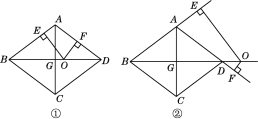
ĢāÄæÄŚČŻ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ĪŅĆĒ¶ØŅåÖ±Ļß![]() ĪŖÅ×ĪļĻß
ĪŖÅ×ĪļĻß![]() ”¢b”¢cĪŖ³£Źż£¬
”¢b”¢cĪŖ³£Źż£¬![]() µÄ”°ĆĪĻėÖ±Ļß”±£»ÓŠŅ»øö¶„µćŌŚÅ×ĪļĻßÉĻ£¬ĮķÓŠŅ»øö¶„µćŌŚyÖįÉĻµÄČż½ĒŠĪĪŖĘä”°ĆĪĻėČż½ĒŠĪ”±£®
µÄ”°ĆĪĻėÖ±Ļß”±£»ÓŠŅ»øö¶„µćŌŚÅ×ĪļĻßÉĻ£¬ĮķÓŠŅ»øö¶„µćŌŚyÖįÉĻµÄČż½ĒŠĪĪŖĘä”°ĆĪĻėČż½ĒŠĪ”±£®

ŅŃÖŖÅ×ĪļĻß![]() ÓėĘä”°ĆĪĻėÖ±Ļß”±½»ÓŚA”¢BĮ½µć
ÓėĘä”°ĆĪĻėÖ±Ļß”±½»ÓŚA”¢BĮ½µć![]() µćAŌŚµćBµÄ×ó²ą
µćAŌŚµćBµÄ×ó²ą![]() £¬ÓėxÖįøŗ°ėÖį½»ÓŚµćC£®
£¬ÓėxÖįøŗ°ėÖį½»ÓŚµćC£®
![]() ĢīæÕ£ŗøĆÅ×ĪļĻߵĔ°ĆĪĻėÖ±Ļß”±µÄ½āĪöŹ½ĪŖ______£¬µćAµÄ×ų±źĪŖ______£¬µćBµÄ×ų±źĪŖ______£»
ĢīæÕ£ŗøĆÅ×ĪļĻߵĔ°ĆĪĻėÖ±Ļß”±µÄ½āĪöŹ½ĪŖ______£¬µćAµÄ×ų±źĪŖ______£¬µćBµÄ×ų±źĪŖ______£»
![]() ČēĶ¼£¬µćMĪŖĻ߶ĪCBÉĻŅ»¶Æµć£¬½«
ČēĶ¼£¬µćMĪŖĻ߶ĪCBÉĻŅ»¶Æµć£¬½«![]() ŅŌAMĖłŌŚÖ±ĻßĪŖ¶Ō³ĘÖį·ÕŪ£¬µćCµÄ¶Ō³ĘµćĪŖN£¬Čō
ŅŌAMĖłŌŚÖ±ĻßĪŖ¶Ō³ĘÖį·ÕŪ£¬µćCµÄ¶Ō³ĘµćĪŖN£¬Čō![]() ĪŖøĆÅ×ĪļĻߵĔ°ĆĪĻėČż½ĒŠĪ”±£¬ĒóµćNµÄ×ų±ź£»
ĪŖøĆÅ×ĪļĻߵĔ°ĆĪĻėČż½ĒŠĪ”±£¬ĒóµćNµÄ×ų±ź£»
![]() µ±µćEŌŚÅ×ĪļĻߵĶŌ³ĘÖįÉĻŌĖ¶ÆŹ±£¬ŌŚøĆÅ×ĪļĻߵĔ°ĆĪĻėÖ±Ļß”±ÉĻ£¬ŹĒ·ń“ęŌŚµćF£¬Ź¹µĆŅŌµćA”¢C”¢E”¢FĪŖ¶„µćµÄĖıߊĪĪŖĘ½ŠŠĖıߊĪ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćE”¢FµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µ±µćEŌŚÅ×ĪļĻߵĶŌ³ĘÖįÉĻŌĖ¶ÆŹ±£¬ŌŚøĆÅ×ĪļĻߵĔ°ĆĪĻėÖ±Ļß”±ÉĻ£¬ŹĒ·ń“ęŌŚµćF£¬Ź¹µĆŅŌµćA”¢C”¢E”¢FĪŖ¶„µćµÄĖıߊĪĪŖĘ½ŠŠĖıߊĪ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćE”¢FµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©![]() £»
£»![]() £»
£»![]() £»£Ø2£©Nµć×ų±źĪŖ
£»£Ø2£©Nµć×ų±źĪŖ![]() »ņ
»ņ![]() £»£Ø3£©
£»£Ø3£©![]() ”¢
”¢![]() »ņ
»ņ![]() ”¢
Ӣ![]()
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ÓÉĆĪĻėÖ±ĻߵĶØŅåæÉĒóµĆĘä½āĪöŹ½£¬ĮŖĮ¢ĆĪĻėÖ±ĻßÓėÅ×ĪļĻß½āĪöŹ½æÉĒóµĆA”¢BµÄ×ų±ź£»
£Ø2£©µ±NµćŌŚyÖįÉĻŹ±£¬¹żA×÷AD”ĶyÖįÓŚµćD£¬ŌņæÉÖŖAN=AC£¬½įŗĻAµć×ų±ź£¬ŌņæÉĒóµĆONµÄ³¤£¬æÉĒóµĆNµć×ų±ź£»µ±MµćŌŚyÖįÉĻ¼“MµćŌŚŌµćŹ±£¬¹żN×÷NP”ĶxÖįÓŚµćP£¬ÓÉĢõ¼žæÉĒóµĆ”ĻNMP=60”ć£¬ŌŚRt”÷NMPÖŠ£¬æÉĒóµĆMPŗĶNPµÄ³¤£¬ŌņæÉĒóµĆNµć×ų±ź£»
£Ø3£©µ±ACĪŖĘ½ŠŠĖıߊĪµÄŅ»±ßŹ±£¬¹żF×÷¶Ō³ĘÖįµÄ“¹ĻßFH£¬¹żA×÷AK”ĶxÖįÓŚµćK£¬æÉÖ¤”÷EFH”Õ”÷ACK£¬æÉĒóµĆDFµÄ³¤£¬ŌņæÉĒóµĆFµćµÄŗį×ų±ź£¬“Ó¶ųæÉĒóµĆFµć×ų±ź£¬ÓÉHEµÄ³¤æÉĒóµĆEµć×ų±ź£»µ±ACĪŖĘ½ŠŠĖıߊĪµÄ¶Ō½ĒĻߏ±£¬ÉčE£Ø©1£¬t£©£¬ÓÉA”¢CµÄ×ų±źæɱķŹ¾³öACÖŠµć£¬“Ó¶ųæɱķŹ¾³öFµćµÄ×ų±ź£¬“śČėÖ±ĻßABµÄ½āĪöŹ½æÉĒóµĆtµÄÖµ£¬æÉĒóµĆE”¢FµÄ×ų±ź£®
£Ø1£©”ßÅ×ĪļĻß![]() £¬”ąĘäĆĪĻėÖ±ĻߵĽāĪöŹ½ĪŖ
£¬”ąĘäĆĪĻėÖ±ĻߵĽāĪöŹ½ĪŖ![]() £¬ĮŖĮ¢ĆĪĻėÖ±ĻßÓėÅ×ĪļĻß½āĪöŹ½æÉµĆ£ŗ
£¬ĮŖĮ¢ĆĪĻėÖ±ĻßÓėÅ×ĪļĻß½āĪöŹ½æÉµĆ£ŗ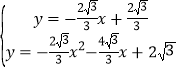 £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() »ņ
»ņ![]() £¬”ąA£Ø©2£¬
£¬”ąA£Ø©2£¬![]() £©£¬B£Ø1£¬0£©£¬¹Ź“š°øĪŖ£ŗ
£©£¬B£Ø1£¬0£©£¬¹Ź“š°øĪŖ£ŗ![]() £»£Ø©2£¬
£»£Ø©2£¬![]() £©£»£Ø1£¬0£©£»
£©£»£Ø1£¬0£©£»
£Ø2£©µ±µćNŌŚyÖįÉĻŹ±£¬”÷AMNĪŖĆĪĻėČż½ĒŠĪ£¬ČēĶ¼1£¬¹żA×÷AD”ĶyÖįÓŚµćD£¬ŌņAD=2£¬ŌŚ![]() ÖŠ£¬Įīy=0æÉĒóµĆx=©3»ņx=1£¬”ąC£Ø©3£¬0£©£¬ĒŅA£Ø©2£¬
ÖŠ£¬Įīy=0æÉĒóµĆx=©3»ņx=1£¬”ąC£Ø©3£¬0£©£¬ĒŅA£Ø©2£¬![]() £©£¬”ąAC=
£©£¬”ąAC=![]() =
=![]() £¬ÓÉ·ÕŪµÄŠŌÖŹæÉÖŖAN=AC=
£¬ÓÉ·ÕŪµÄŠŌÖŹæÉÖŖAN=AC=![]() £¬ŌŚRt”÷ANDÖŠ£¬Óɹ“¹É¶ØĄķæɵĆDN=
£¬ŌŚRt”÷ANDÖŠ£¬Óɹ“¹É¶ØĄķæɵĆDN=![]() =
=![]() =3£¬”ßOD=
=3£¬”ßOD=![]() £¬”ąON=
£¬”ąON=![]() ©3»ņON=
©3»ņON=![]() +3£¬µ±ON=
+3£¬µ±ON=![]() +3Ź±£¬ŌņMN£¾OD£¾CM£¬ÓėMN=CMƬ¶Ü£¬²»ŗĻĢāŅā£¬”ąNµć×ų±źĪŖ£Ø0£¬
+3Ź±£¬ŌņMN£¾OD£¾CM£¬ÓėMN=CMƬ¶Ü£¬²»ŗĻĢāŅā£¬”ąNµć×ų±źĪŖ£Ø0£¬![]() ©3£©£»
©3£©£»
µ±MµćŌŚyÖįÉĻŹ±£¬ŌņMÓėOÖŲŗĻ£¬¹żN×÷NP”ĶxÖįÓŚµćP£¬ČēĶ¼2£¬ŌŚRt”÷AMDÖŠ£¬AD=2£¬OD=![]() £¬”ątan”ĻDAM=
£¬”ątan”ĻDAM=![]() =
=![]() £¬”ą”ĻDAM=60”ć£¬”ßAD”ĪxÖį£¬”ą”ĻAMC=”ĻDAO=60”ć£¬ÓÖÓÉÕŪµžæÉÖŖ”ĻNMA=”ĻAMC=60”ć£¬”ą”ĻNMP=60”ć£¬ĒŅMN=CM=3£¬”ąMP=
£¬”ą”ĻDAM=60”ć£¬”ßAD”ĪxÖį£¬”ą”ĻAMC=”ĻDAO=60”ć£¬ÓÖÓÉÕŪµžæÉÖŖ”ĻNMA=”ĻAMC=60”ć£¬”ą”ĻNMP=60”ć£¬ĒŅMN=CM=3£¬”ąMP=![]() MN=
MN=![]() £¬NP=
£¬NP=![]() MN=
MN=![]() £¬”ą“ĖŹ±Nµć×ų±źĪŖ£Ø
£¬”ą“ĖŹ±Nµć×ų±źĪŖ£Ø![]() £¬
£¬![]() £©£»
£©£»
×ŪÉĻæÉÖŖNµć×ų±źĪŖ£Ø0£¬![]() ©3£©»ņ£Ø
©3£©»ņ£Ø![]() £¬
£¬![]() £©£»
£©£»
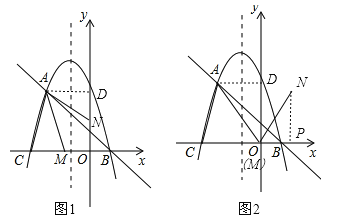
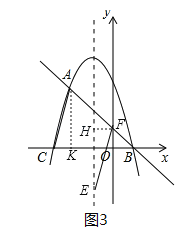
£Ø3£©¢Łµ±ACĪŖĘ½ŠŠĖıߊĪµÄ±ßŹ±£¬ČēĶ¼3£¬¹żF×÷¶Ō³ĘÖįµÄ“¹ĻßFH£¬¹żA×÷AK”ĶxÖįÓŚµćK£¬ŌņÓŠAC”ĪEFĒŅAC=EF£¬”ą”ĻACK=”ĻEFH£¬ŌŚ”÷ACKŗĶ”÷EFHÖŠ£¬”ß”ĻACK=”ĻEFH£¬”ĻAKC=”ĻEHF£¬AC=EF£¬”ą”÷ACK”Õ”÷EFH£ØAAS£©£¬”ąFH=CK=1£¬HE=AK=![]() £¬”ßÅ×ĪļĻ߶Ō³ĘÖįĪŖx=©1£¬”ąFµćµÄŗį×ų±źĪŖ0»ņ©2£¬”ßµćFŌŚÖ±ĻßABÉĻ£¬”ąµ±Fµćŗį×ų±źĪŖ0Ź±£¬ŌņF£Ø0£¬
£¬”ßÅ×ĪļĻ߶Ō³ĘÖįĪŖx=©1£¬”ąFµćµÄŗį×ų±źĪŖ0»ņ©2£¬”ßµćFŌŚÖ±ĻßABÉĻ£¬”ąµ±Fµćŗį×ų±źĪŖ0Ź±£¬ŌņF£Ø0£¬![]() £©£¬“ĖŹ±µćEŌŚÖ±ĻßABĻĀ·½£¬”ąEµ½yÖįµÄ¾ąĄėĪŖEH©OF=
£©£¬“ĖŹ±µćEŌŚÖ±ĻßABĻĀ·½£¬”ąEµ½yÖįµÄ¾ąĄėĪŖEH©OF=![]() ©
©![]() =
=![]() £¬¼“Eµćׯ×ų±źĪŖ©
£¬¼“Eµćׯ×ų±źĪŖ©![]() £¬”ąE£Ø©1£¬©
£¬”ąE£Ø©1£¬©![]() £©£»
£©£»
µ±FµćµÄŗį×ų±źĪŖ©2Ź±£¬ŌņFÓėAÖŲŗĻ£¬²»ŗĻĢāŅā£¬ÉįČ„£»
¢Śµ±ACĪŖĘ½ŠŠĖıߊĪµÄ¶Ō½ĒĻߏ±£¬”ßC£Ø©3£¬0£©£¬ĒŅA£Ø©2£¬![]() £©£¬”ąĻ߶ĪACµÄÖŠµć×ų±źĪŖ£Ø©2.5£¬
£©£¬”ąĻ߶ĪACµÄÖŠµć×ų±źĪŖ£Ø©2.5£¬![]() £©£¬ÉčE£Ø©1£¬t£©£¬F£Øx£¬y£©£¬Ōņx©1=2”Į£Ø©2.5£©£¬y+t=
£©£¬ÉčE£Ø©1£¬t£©£¬F£Øx£¬y£©£¬Ōņx©1=2”Į£Ø©2.5£©£¬y+t=![]() £¬”ąx=©4£¬y=
£¬”ąx=©4£¬y=![]() ©t£¬“śČėÖ±ĻßAB½āĪöŹ½æɵĆ
©t£¬“śČėÖ±ĻßAB½āĪöŹ½æɵĆ![]() ©t=©
©t=©![]() ”Į£Ø©4£©+
”Į£Ø©4£©+![]() £¬½āµĆt=©
£¬½āµĆt=©![]() £¬”ąE£Ø©1£¬©
£¬”ąE£Ø©1£¬©![]() £©£¬F£Ø©4£¬
£©£¬F£Ø©4£¬![]() £©£»
£©£»
×ŪÉĻæÉÖŖ“ęŌŚĀś×ćĢõ¼žµÄµćF£¬“ĖŹ±E£Ø©1£¬©![]() £©”¢F£Ø0£¬
£©”¢F£Ø0£¬![]() £©»ņE£Ø©1£¬©
£©»ņE£Ø©1£¬©![]() £©”¢F£Ø©4£¬
£©”¢F£Ø©4£¬![]() £©£®
£©£®

 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø