题目内容
【题目】补全下列解题过程：
如图，OD是∠AOC的平分线，且∠BOC-∠AOB=40°，若∠AOC=120°，求∠BOD的度数.
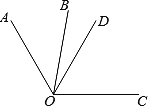
解：∵OD是∠AOC的平分线,∠AOC=120°
∴∠DOC=
∠_______=______°.
∵∠BOC+∠_____=120°，∠BOC-∠AOB=40°
∴∠BOC=80°
∴∠BOD=∠BOC-∠______=______°
【答案】见解析.
【解析】
先根据角平分线的定义求出∠DOC的度数，再由∠BOC+∠AOB=120°，∠BOC-∠AOB=40°得出∠BOC的度数，根据∠BOD=∠BOC-∠DOC即可得出结论．
∵OD是∠AOC的平分线，∠AOC=120°，
∴∠DOC=
∠AOC=60°．
∵∠BOC+∠AOB=120°，∠BOC-∠AOB=40°，
∴∠BOC=80°．
∴∠BOD=∠BOC-∠DOC=20°；
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
【题目】某班在一次班会课上，就“遇见路人摔倒后如何处理”的主题进行讨论，并对全班 50 名学生的处理方式进行统计，得出相关统计表和统计图．
组别 | A | B | C | D |
处理方式 | 迅速离开 | 马上救助 | 视情况而定 | 只看热闹 |
人数 | m | 30 | n | 5 |
请根据表图所提供的信息回答下列问题：
(1)统计表中的 m＝ ，n＝ ；
(2)补全频数分布直方图；
(3)若该校有 2000 名学生，请据此估计该校学生采取“马上救助”方式的学生有多少人？
