题目内容
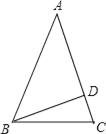
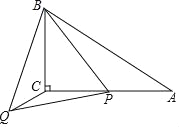
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点P是AC上的动点,连接BP,以BP为边作等边△BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是______.
【答案】![]() .
.
【解析】
如图,取AB的中点E,连接CE,PE.由△QBC≌△PBE(SAS),推出QC=PE,推出当EP⊥AC时,QC的值最小;
解:如图,取AB的中点E,连接CE,PE.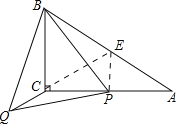
∵∠ACB=90°,∠A=30°,
∴∠CBE=60°,
∵BE=AE,
∴CE=BE=AE,
∴△BCE是等边三角形,
∴BC=BE,
∵∠PBQ=∠CBE=60°,
∴∠QBC=∠PBE,
∵QB=PB,CB=EB,
∴△QBC≌△PBE(SAS),
∴QC=PE,
∴当EP⊥AC时,QC的值最小,
在Rt△AEP中,∵AE=![]() ,∠A=30°,
,∠A=30°,
∴PE=![]() AE=
AE=![]() ,
,
∴CQ的最小值为![]() .
.
故答案为:![]()

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目