题目内容
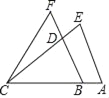
【题目】如图,已知AB=2,BF=8,BC=AE=6,CE=CF=7,则△CDF与四边形ABDE的面积比值是( )
A. 1:1 B. 2:1 C. 1:2 D. 2:3
【答案】A
【解析】
由题意得AC=CB+BA=8,可得AC=BF,利用SSS可证得△AEC≌△BCF,从而可得S△AEC=S△BCF,也就得出S△CDF+S△CDB=S四边形ABDE+S△CDB,这样可求出四边形ABDE与△CDF面积的比值.
解:∵AB=2,BF=8,BC=AE=6,
∴AC=CB+BA=8,
∴AC=BF,
在△AEC和△BCF中,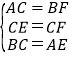
∴△AEC≌△BCF(SSS),
∴S△AEC=S△BCF,
∴S△CDF+S△CDB=S四边形ABDE+S△CDB
∴S四边形ABDE=S△CDF,
∴四边形ABDE与△CDF面积的比值是1:1.
故选:A.

【题目】某年级共有330名男生,为了解该年级男生1000米跑步成绩(单位:分/秒)的情况,从中随机抽取30名男生进行测试,获得了他们的相关成绩,并对数据进行整理、描述和分析.下面给出了部分信息.
a.1000米跑步的频数分布表如下:
分组 | 3′17″<x≤3′ 37″ | 3′37″<x≤3′ 57″ | 3′ 57″<x≤4′ 17″ | 4′ 17″<x≤4′ 37″ | 4′ 37″<x≤4′ 57″ | 4′ 57″<x≤5′ 17″ |
频数 | 10 | 9 | m | 2 | 2 | 1 |
注:3′37″即3分37秒
b.1000米跑步在3′37″<x≤3′57″这一组是:
3′39 ″ 3′42 ″ 3′45 ″ 3′45″ 3′50 ″ 3′52 ″ 3′53″ 3′55″ 3′57″
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)根据表频数分布表画出相应的频数分布直方图.
(3)若男生1000米跑步成绩等于或者优于3′52″,成绩记为优秀.请估计全年级男生跑步成绩达到优秀的人数.