题目内容
【题目】(1)已知一个多边形的内角和是它的外角和的 3 倍,求这个多边形的边数.
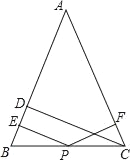
(2)如图,点F 是△ABC 的边 BC 延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF 的度数.

【答案】(1)8;(2)80°.
【解析】
根据多边形的外角和为360°,内角和公式为:(n-2)180°,由题意可知:内角和=3×外角和,设出未知数,可得到方程,解方程即可.
在直角三角形DFB中,根据三角形内角和定理,求得∠B的度数;再在△ABC中,根据内角与外角的性质求∠ACF的度数即可.
(1)设这个多边形的边数为n,
∵n边形的内角和为(n﹣2)180°,多边形的外角和为360°,
∴(n﹣2)180°=360°×3,
解得n=8.
∴这个多边形的边数为8.
(2)在△DFB中,
∵DF⊥AB,
∴∠FDB=90°,
∵∠F=40°,∠FDB+∠F+∠B=180°,
∴∠B=50°.
在△ABC中,
∵∠A=30°,∠B=50°,
∴∠ACF=30°+50°=80°.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目