题目内容
(1)探索归纳.用等号或不等号填空:
①5+6______2
②12+13______2
③5+0______2
④7+7______2
…
用非负数a、b表示你发现的规律并予以证明.
(2)结论应用.已知点A(-3,0),B(0,-4),P是双曲线y=
(x>0)上任意一点,过点P作PC⊥x轴于C,过点p作PD⊥y轴于D,连接AB、BC、CD、DA.
求四边形ABCD的面积的最小值,并说明此时四边形ABCD的形状.

①5+6______2
| 5×6 |
②12+13______2
| 12×13 |
③5+0______2
| 5×0 |
④7+7______2
| 7×7 |
用非负数a、b表示你发现的规律并予以证明.
(2)结论应用.已知点A(-3,0),B(0,-4),P是双曲线y=
| 12 |
| x |
求四边形ABCD的面积的最小值,并说明此时四边形ABCD的形状.

(1)①∵5+6=11,2
=
,120<121,
∴11>2
;
②∵12+13=25,2
=
<
=25,
∴12+13>2
;
③∵5+0=5,2
=0,
∴5+0>2
;
④∵7+7=14,2
=14,
∴7+7=2
.
综上所述,若a、b为非负数,则a+b≥2
.
证明:∵(
-
)2≥0,
∴a-2
+b≥0,
∴a+b≥2
,只有点a=b时,等号成立.
故答案为:>;>;>;=;
(2)∵设P(x,
),则C(x,0),D(0,
),CA=x+3,DB=+4,
∴S四边形ABCD=
CA×DB=
(x+3)×(
+4),
化简得:S=2(x+
)+12,
∵x>0,
>0,
∴x+
≥2
=6,
只有当x=
,即x=3时,等号成立.
∴S≥2×6+12=24,
∴S四边形ABCD有最小值24,
此时,P(3,4),C(3,0),D(0,4),AB=BC=CD=DA=5,
∴四边形ABCD是菱形.
| 5×6 |
| 120 |
∴11>2
| 5×6 |
②∵12+13=25,2
| 12×13 |
| 624 |
| 625 |
∴12+13>2
| 12×13 |
③∵5+0=5,2
| 5×0 |
∴5+0>2
| 5×0 |
④∵7+7=14,2
| 7×7 |
∴7+7=2
| 7×7 |
综上所述,若a、b为非负数,则a+b≥2
| ab |
证明:∵(
| a |
| b |
∴a-2
| ab |
∴a+b≥2
| ab |
故答案为:>;>;>;=;
(2)∵设P(x,
| 12 |
| x |
| 12 |
| x |
∴S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| x |
化简得:S=2(x+
| 9 |
| x |
∵x>0,
| 9 |
| x |
∴x+
| 9 |
| x |
x×
|
只有当x=
| 9 |
| x |
∴S≥2×6+12=24,
∴S四边形ABCD有最小值24,
此时,P(3,4),C(3,0),D(0,4),AB=BC=CD=DA=5,
∴四边形ABCD是菱形.

练习册系列答案
相关题目



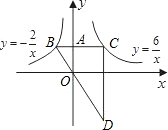 <0)的图象于B,交函数y=
<0)的图象于B,交函数y=


