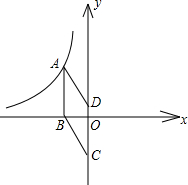
题目内容
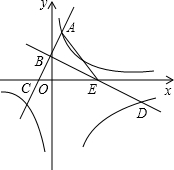
如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A,B,与反比例函数y=
(k为常数,且k>0)在第一象限的图象交于点E,m.过点E作EM⊥y轴于M,过点m作m0⊥x轴于0,直线EM与m0交于点C.若
=
(m为大于l的常数).记△CEm的面积为S1,△OEm的面积为S2,则
=______.&0bsp;(用含m的代数式表示)

| k |
| x |
| BE |
| Bm |
| 1 |
| m |
| S1 |
| S2 |

过点F作FD⊥cO于点D,EW⊥AO于点W,
∵
=
,
∴
=
,
∵9E•EW=FN•DF,
∴
=
,
∴
=
,
设E点坐标为:(6,9r),则F点坐标为:(96,r),
∴△CEF的面积为:S9=
(96-6)(9r-r)=
(9-9)26r,
∵△OEF的面积为:S2=S矩形CNO9-S9-S△9EO-S△FON,
=9C•CN-
(9-9)26r-
9E•9O-
FN•NO,
=96•9r-
(9-9)26r-
6•9r-
r•96,
=926r-
(9-9)26r-96r,
=
(92-9)6r,
=
(9+9)(9-9)6r,
∴
=
=
.
故答案为:
.
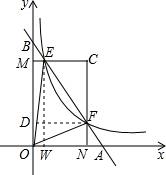
∵
| cE |
| cF |
| 9 |
| 9 |
∴
| 9E |
| DF |
| 9 |
| 9 |
∵9E•EW=FN•DF,
∴
| 9E |
| DF |
| FN |
| EW |
∴
| FN |
| EW |
| 9 |
| 9 |
设E点坐标为:(6,9r),则F点坐标为:(96,r),
∴△CEF的面积为:S9=
| 9 |
| 2 |
| 9 |
| 2 |
∵△OEF的面积为:S2=S矩形CNO9-S9-S△9EO-S△FON,
=9C•CN-
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
=96•9r-
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
=926r-
| 9 |
| 2 |
=
| 9 |
| 2 |
=
| 9 |
| 2 |
∴
| S9 |
| S2 |
| ||
|
| 9-9 |
| 9+9 |
故答案为:
| 9-9 |
| 9+9 |


练习册系列答案
相关题目
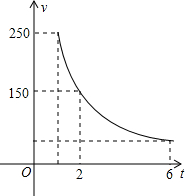
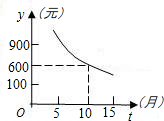 时间t的关系如图所示:
时间t的关系如图所示: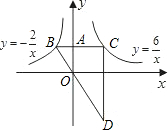 <0)的图象于B,交函数y=
<0)的图象于B,交函数y=