题目内容
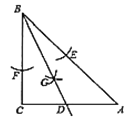
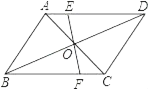
【题目】如图,已知△ABC,点D、E分别在边AC、AB上,∠ABD=∠ACE,下列条件中,不能判定△ABC是等腰三角形的是( )

A. AE=AD;B. BD=CE;C. ∠ECB=∠DBC ;D. ∠BEC=∠CDB.
【答案】D
【解析】
添加AE=AD、BD=CE、∠ECB=∠DBC可利用AAS判定△ABD≌△ACE,进而可得AB=AC,从而可得△ABC是等腰三角形;添加∠BEC=∠CDB不能判定△ABD≌△ACE,因此也不能证明AB=AC,进而不能证明△ABC是等腰三角形.
A、添加AE=AD,
在△ABD和△ACE中
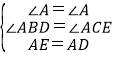 ,
,
∴△ABD≌△ACE(AAS),
∴AB=AC,
∴△ABC为等腰三角形,故此选项不合题意;
B、添加BD=CE,
在△ABD和△ACE中
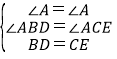 ,
,
∴△ABD≌△ACE(AAS),
∴AB=AC,
∴△ABC为等腰三角形,故此选项不合题意;
C、添加∠ECB=∠DBC,
又∵∠ABD=∠ACE,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC为等腰三角形,故此选项不合题意;
D、添加∠BEC=∠CDB,不能证明△ABD≌△ACE,因此也不能证明AB=AC,进而得不到△ABC为等腰三角形,故此选项符合题意;
故选D.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目