题目内容
【题目】将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1,点A、C、D的对应点分别为A1、C1、D1
(1)当点A1落在AC上时
①如图1,若∠CAB=60°,求证:四边形ABD1C为平行四边形;
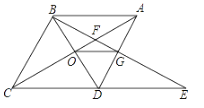
②如图2,AD1交CB于点O.若∠CAB≠60°,求证:DO=AO;
(2)如图3,当A1D1过点C时.若BC=5,CD=3,直接写出A1A的长.

【答案】(1)①证明见解析;②证明见解析;(2)![]()
【解析】
(1)①首先证明△ABA1是等边三角形,可得∠AA1B=∠A1BD1=60°,即可解决问题.
②首先证明△OCD1≌△OBA(AAS),推出OC=OB,再证明△DCO≌△ABO(SAS)即可解决问题.
(2)如图3中,作A1E⊥AB于E,A1F⊥BC于F.利用勾股定理求出AE,A1E即可解决问题.
(1)证明:①如图1中,
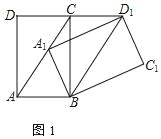
∵∠BAC=60°,BA=BA1,
∴△ABA1是等边三角形,
∴∠AA1B=60°,
∵∠A1BD1=60°,
∴∠AA1B=∠A1BD1,
∴AC∥BD1,
∵AC=BD1,
∴四边形ABD1C是平行四边形.
②如图2中,连接BD1.
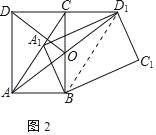
∵四边形ABD1C是平行四边形,
∴CD1∥AB,CD1=AB,
∠OCD1=∠ABO,
∵∠COD1=∠AOB,
∴△OCD1≌△OBA(AAS),
∴OC=OB,
∵CD=BA,∠DCO=∠ABO,
∴△DCO≌△ABO(SAS),
∴DO=OA.
(2)如图3中,作A1E⊥AB于E,A1F⊥BC于F.
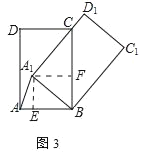
在Rt△A1BC中,∵∠CA1B=90°,BC=5.AB=3,
∴CA1=![]() =4,
=4,
∵![]() A1CA1B=
A1CA1B=![]() BCA1F,
BCA1F,
∴A1F=![]() ,
,
∵∠A1FB=∠A1EB=∠EBF=90°,
∴四边形A1EBF是矩形,
∴EB=A1F=![]() ,A1E=BF=
,A1E=BF=![]() ,
,
∴AE=3﹣![]() =
=![]() ,
,
在Rt△AA1E中,AA/span>1=![]() =
=![]() .
.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案【题目】平某游泳馆暑期推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费20元;方式二:不购买会员证,每次游泳付费25元.设小明计划今年暑期游泳次数为x(x为正整数).根据题意列表:
游泳次数 | 5 | 8 | 10 | … | x |
方式一的总费用( | 200 | 260 | m | … | |
方式二的总费用( | 125 | 200 | 250 | … |
(1)表格中的m值为 ;
(2)根据题意分别求出两种付费方式中![]() 与自变量x之间的函数关系式并画出图象;
与自变量x之间的函数关系式并画出图象;
(3)请你根据图象,帮助小明设计一种比较省钱的付费方案.