Question

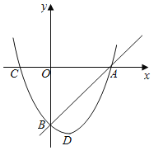
【题目】如图，抛物线的图象与x轴交A（-3，0），B（1，0）两点，与y轴交于点C（0，3），点D为抛物线的顶点．

（1）求抛物线的解析式；

（2）设点T在第二象限的抛物线上，若其关于原点的对称点也在抛物线上，求点T的坐标；

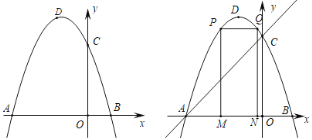
（3）点M为线段AB上一点（点M不与点A，B重合），过M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过P作PQ∥AB交抛物线于点Q，过Q作QN⊥x轴于N，当矩形PMNQ的周长最大时，求△AEM的面积．

Answer 1

【答案】（1）y=-x2-2x+3；（2）T（-，2）；（3）．

【解析】

（1）用待定系数法，即可求出解析式；

（2）设点T坐标，表示出点T关于原点对称的点，代入解析式，求出点T坐标；

（3）设M点横坐标为m，则PM=-m2-2m+3，MN=（-m-1）×2=-2m-2，矩形PMNQ的周长=-2m2-8m+2，将-2m2-8m+2配方，根据二次函数的性质，即可得出m的值，然后求得直线AC的解析式，把x=m代入可以求得E点坐标，从而求得三角形的面积．

解：（1）设解析式y=a（x-1）（x+3）

将C（0，3）代入得a =-1

∴解析式为y=-x2-2x+3

（2）设T（m，-m2-2m+3）

则点T关于原点对称的点K坐标为（-m，m2+2m-3）

将点K代入解析式得

m2+2m-3=-m2+2m+3

∴m2=3

∴m=±

∴m=-

∴T（-，2）

（3）由抛物线y=-x2-2x+3=-（x+1）2+4可知，对称轴为直线x=-1，设点M的横坐标为m，则PM=-m2-2m+3，MN=（-m-1）×2=-2m-2，

∴矩形PMNQ的周长=2（PM+MN）=2（-m2-2m+3-2m-2）=-2m2-8m+2=-2（m+2）2+10，

∴当m=-2时矩形的周长最大．

∵点A（-3，0），C（0，3），

∴直线AC的函数表达式为y=x+3，

当x=-2时，y=-2+3=1，则点E（-2，1），

∴EM=1，AM=1，

∴S=AMEM=．