题目内容
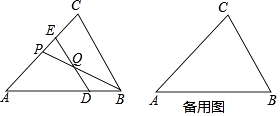
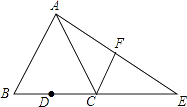
【题目】如图，△ABC边AB上点D、E（不与点A、B重合），满足∠DCE=∠ABC，∠ACB=90°，AC=3，BC=4； 
（1）当CD⊥AB时，求线段BE的长；
（2）当△CDE是等腰三角形时，求线段AD的长；
（3）设AD=x，BE=y，求y关于x的函数解析式，并写出定义域．
【答案】
（1）解：在△ABC中，∠ACB=90°，AC=3，BC=4，
∴AB=5，sinA= 
，tanB= 
，
如图，当CD⊥AB时，△ACD为直角三角形，
∴CD=ACsinA= 
，
∴AD= 
= 
，
又∵∠DCE=∠ABC，
∴在Rt△CDE中，DE=CDtan∠DCE= × = ，
∴BE=AB﹣AD﹣DE=5﹣ ﹣ = 
（2）解：当△CDE时等腰三角形时，可知∠CDE＞∠A＞∠B=∠DCE，∠CED＞∠B=∠DCE，
∴唯有∠CED=∠CDE，
又∵∠B=∠DCE，∠CDE=∠BDC，
∴∠BCD=∠CED=∠CDE=∠BDC，
∴BD=BC=4，
∴AD=5﹣4=1
（3）解：如图所示，作CH⊥AB于H，
∵ 
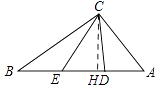
×BC×AC= AB×CH，
∴CH= ，
∴Rt△ACH中，AH= 
= ，
∴在Rt△CDH中，CD2=CH2+DH2=（ ）2+（ ﹣x）2=x2﹣ 
x+9，
又∵∠CDE=∠BDC，∠DCE=∠B，
∴△BDC∽△CDE，
∴CD2=DEDB，
即x2﹣ x+9=（5﹣x﹣y）（5﹣x），
解得 
．
【解析】（1）先根据∠ACB=90°，AC=3，BC=4，求得AB=5，sinA= ，tanB= 
，再根据△ACD为直角三角形，求得AD，在Rt△CDE中，求得DE，最后根据BE=AB﹣AD﹣DE进行计算即可；（2）当△CDE时等腰三角形时，可知∠CDE＞∠A＞∠B=∠DCE，∠CED＞∠B=∠DCE，进而得出∠CED=∠CDE，再根据∠B=∠DCE，∠CDE=∠BDC，得到∠BCD=∠CED=∠CDE=∠BDC，最后求得AD的长；（3）先作CH⊥AB于H，Rt△ACH中，求得CH和AH的长，在Rt△CDH中，根据勾股定理得出：CD2=x2﹣ x+9，再判定△BDC∽△CDE，得出CD2=DEDB，即x2﹣ x+9=（5﹣x﹣y）（5﹣x），最后求得y关于x的函数解析式，并写出定义域．
【考点精析】认真审题，首先需要了解等腰三角形的性质(等腰三角形的两个底角相等（简称：等边对等角）)，还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键．
