题目内容
【题目】如图,在梯形ABCD中,AD∥BC,AD=3,BC=2,点E、F分别在两腰上, 且EF∥AD,AE:EB=2:1;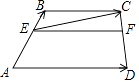
(1)求线段EF的长;
(2)设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,试用
,试用 ![]() 、
、 ![]() 表示向量
表示向量 ![]() .
.
【答案】
(1)解:作BM∥CD交AD、EF于M、N两点,
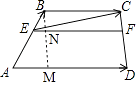
又AD∥BC,EF∥AD,
∴四边形BCFN与MNFD均为平行四边形.
∴BC=NF=MD=2,
∴AM=AD﹣MD=1.
又 ![]() =2,
=2,
∴ ![]() =
= ![]() ,
,
∵EF∥AD,
∴△BEN∽△BAM,
∴ ![]() ,即
,即 ![]() ,
,
∴EN= ![]() ,
,
则EF=EN+NF= ![]()
(2)解:∵ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴BC= ![]() AD,EB=
AD,EB= ![]() AB,
AB,
∴ ![]() =
= ![]()
![]() =
= ![]()
![]() ,
, ![]() =
= ![]()
![]() =
= ![]()
![]() ,
,
则 ![]() =
= ![]() =
= ![]()
![]() +
+ ![]()
![]()
【解析】(1)作BM∥CD交AD、EF于M、N两点,将问题转化到△ABM中,利用相似三角形的判定与性质求EN,由EF=EN+NF=EN+AD进行求解;(2)由 ![]() =
= ![]() 、
、 ![]() =
= ![]() 得BC=
得BC= ![]() AD,EB=
AD,EB= ![]() AB,根据
AB,根据 ![]() =
= ![]() 可得答案.
可得答案.
【考点精析】本题主要考查了梯形的定义的相关知识点,需要掌握一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】某校为了增强学生体质,推动“阳光体育”运动的广泛开展,学校准备购买一批运动鞋供学生借用,学校体育部从八年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和②,请根据相关信息,解答下列问题: 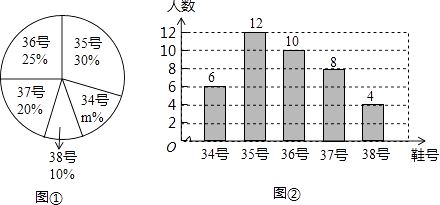
(1)图①中m的值为;
(2)本次调查获取的样本数据的众数是 , 中位数是;
(3)该校计划购买200双运动鞋,校体育部对各种鞋号运动鞋的购买数量做出如下估计:
根据样本数据分析得知:各种鞋号的运动鞋购买数量如下: |
请你分析:校体育部的估计是否合理?如果合理,请将体育部的估算过程补充完整,若不合理,请说明理由,并且给学校提一个合理化的建议.